One of the coolest things about building and studying computers is taking rocks and training them to add and remember numbers. Wow! Rocks usually do not (and should not) know how to add or remember numbers, but we went ahead and made them do it anyway. Go humans!

But you know what’s even cooler than that? Training rocks… that STICK TOGETHER… to do those things too. That’s right – the same sticking-together rocks holding papers onto your cold-making box.

I like to think about sticking-together rocks because they are so weird and interesting. Why do they stick together? Why do other rocks not stick together? Why do so few people know how they work? So many questions, yet so few answers…

Anyway, let’s talk about how these strange rocks work and how we can turn them into computers!

How does a computer work?

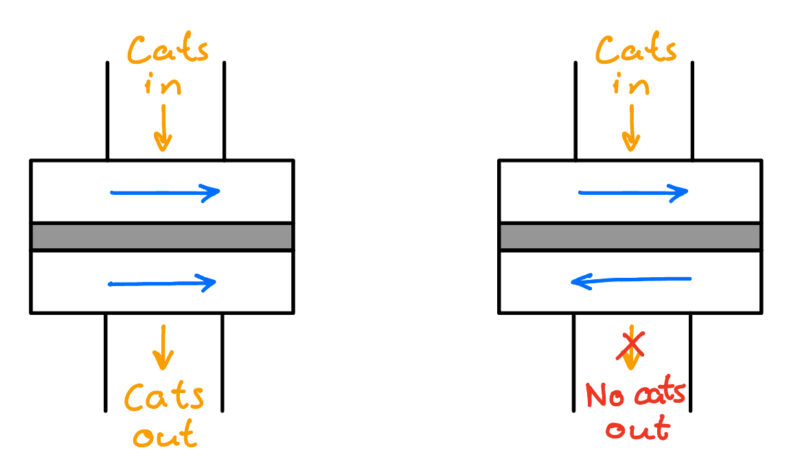
I like to think of a computer as a big house with many doors, and cats walking through the open doors. Each door has a little guy controlling it, and the cats walking around the house can make the little guys open or shut their doors.

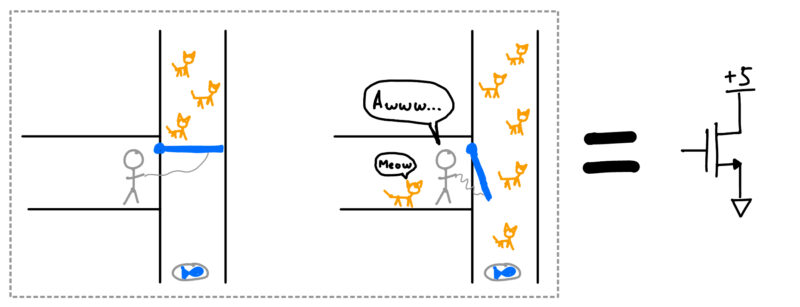
It’s like a cat door, except other cats control it

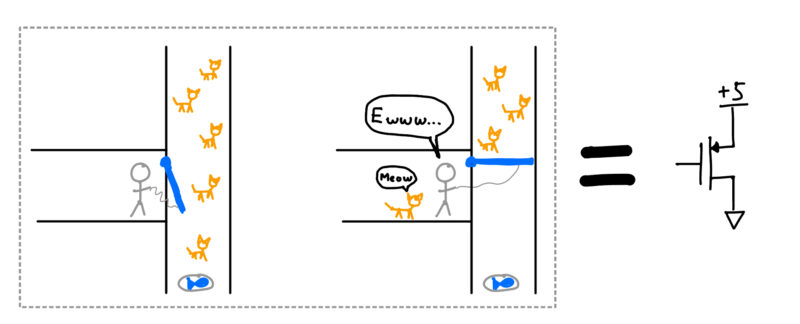
The cat can also make the door close

You can use these doors to control where the cats go in the house. Like this little house where cats will come out of room C only if either room A or room B don’t have cats.

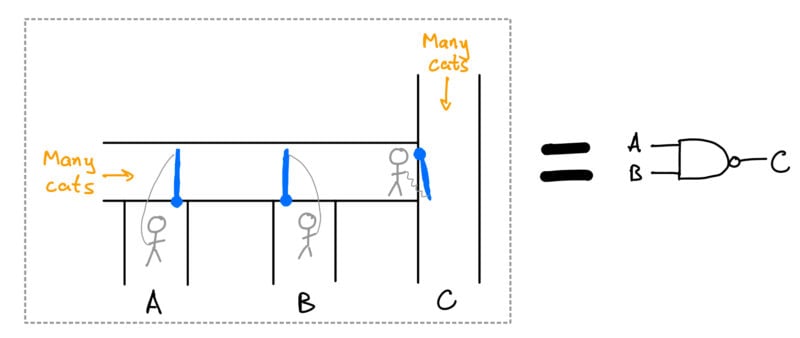
Called a “not and” door

It turns out that you can use this “not and” door to do… well, a lot of things. Like adding numbers:

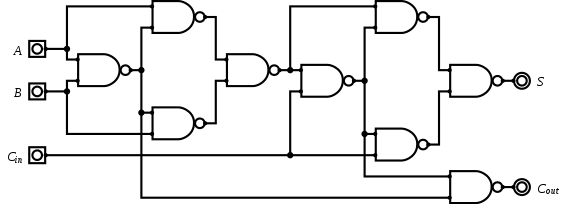
There must be so many cats in this house

Now just stick ten hundred hundred hundred hundred hundred of these doors in the house, and you’ll have yourself a full computer!

How do sticking-together rocks work?

Not all rocks can stick to other rocks or your cool-making box. Most rocks actually do not stick to other rocks (unless you try really hard), and some even push other rocks away.

Why does this happen? And where does this sticking-together force that we can’t see come from? To answer these questions, we have to look at a sticking-together rock up close.

Closer!

EVEN CLOSER!

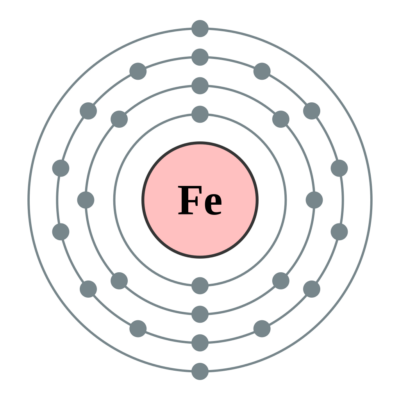
Perfect.

This little piece of the rock is made of two parts: a big ball in the middle and many much smaller balls around it. (Except they’re more like waves than balls sometimes, but pretend that they’re balls for now.) These little balls cause little sticking-together forces in two ways:

1. When they fly around the big ball. (Except they’re not really flying around. But it’s like they’re flying around.)
2. When they turn very fast. (Except they’re not really turning, because if they were, then they’d be faster than light. But it’s like they’re turning.)

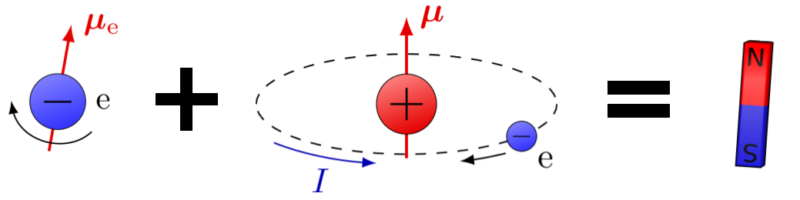
Do you see why sticking-together rocks are so weird now?

In most rocks, these little sticking-together forces point in different directions. Add them up, and you get no total force, so those rocks just sit there and do nothing. But in a few rocks, you can get those forces to point in the same direction and stay that way. Add them up, and you get a big sticking-together force!

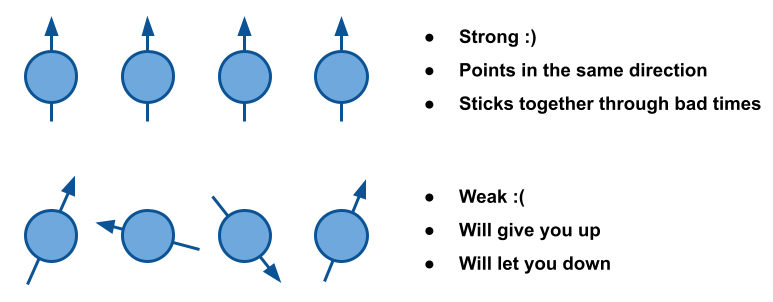
It’s also possible for the forces to point up-down-up-down or even in a three-sided figure, but let’s now worry about these for now. I still don’t quite understand how these kinds of rocks work, and the words I’d need to explain them are really big and definitely in the no-no set of words.

Putting it all together

To make a computer door out of these sticking-together rocks, you need two of them next to each other. Remember how each rock has a force that points in one direction? Imagine now that you have two guys (instead of just one) controlling the door. If both of them push on the door, then it stays shut; but if one of them pulls instead, then the door opens.

So going back to our rocks, if they both point in one direction, then the door is open; else, it is shut! (This isn’t quite exactly what happens, but it’s the right idea.)

We could use this approach to add numbers using these rocks, but it’s usually much easier to use other rocks for that. So instead, we usually use sticking-together rocks to help computers remember numbers.