Did you know? Of all 7,238 MIT Admissions blog posts before this one, only four⁠01 I’m only counting blogs that explicitly use the LaTeX tag in WordPress contain equations typeset in \(\LaTeX\). And they’re all Paolo’s!

That changes today. MIT exposes us to so many beautiful mathematical concepts, so Paige and Fatima have challenged us bloggers to write posts about these concepts this month. To kick off this challenge, let me tell you about duality – a neat little concept that shows up everywhere, from algorithms to superconducting circuits.

What is duality?

As a non-mathematician, I think it’s hard to define duality succinctly yet intuitively. I usually just kind of wave my hands and say, “Uhh, it’s like when two things are different, but they’re actually the same.” So instead of attempting to define it, here’s a concrete example.

Suppose you draw two points on a sheet of paper.

If you want to connect those two points using a straight line, there’s only one way to do it. So we say that two points define a line.

Now suppose you draw two lines on a sheet of paper (but make the lines infinitely long).

Assuming these lines are not parallel, they intersect each other exactly once. So we say that two (non-parallel) lines define a point.

This is a duality! Points and lines are clearly different, but these two statements reveal a striking symmetry between them.

(Minor spoiler for Paige’s post: You can represent points as coordinates \((a, b)\) and lines as equations \(ax – b\). Try turning points into lines and vice versa, and see what happens!)

Duality shows up everywhere in mathematics. Wikipedia lists a few dozen famous examples, and I’m sure there are hundreds more that people have discovered.

Applications to engineering

In addition to being fun to think about, duality is an S-tier mathematical concept to me because it often applies to physical systems and helps simplify complex problems. Specifically, I use duality to analyze electrical circuits.

In physics, electric fields (\(\mathbf{E}\)) and magnetic fields (\(\mathbf{B}\)) are duals. For every equation involving \(\mathbf{E}\), there’s an equivalent equation involving \(\mathbf{B}\), and vice versa. You can see this symmetry in Maxwell’s equations in a vacuum⁠02 The full Maxwell’s equations involve some more stuff, but don’t worry about that for now. :

\(\begin{aligned} \nabla \cdot \mathbf{E} = 0 &\qquad \nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} \\ \nabla \cdot \mathbf{B} = 0 &\qquad \nabla \times \mathbf{B} = \frac{1}{c^2} \frac{\partial \mathbf{E}}{\partial t} \end{aligned}\)

As a result, every circuit component that does something with electrical charge has a dual component that does the same thing with magnetic flux. For example, capacitors (components that store charge) and inductors (components that store flux) are duals:

\(\begin{aligned} i = C \frac{dv}{dt} \iff v = L \frac{di}{dt} \end{aligned}\)

In fact, every circuit has a “dual circuit”, where voltages in the original circuit correspond to currents in the dual circuit, and vice versa:

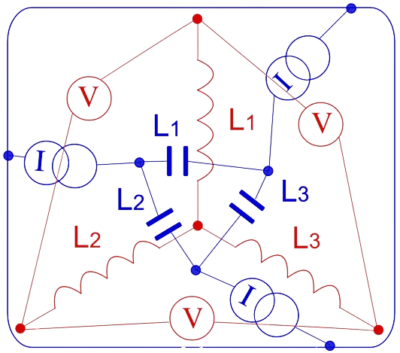
An example of dual circuits taken from Wikipedia

Furthermore, the current (flow of electrical charge) in the dual circuit represents how magnetic flux flows through the original circuit! Again, this is thanks to symmetry:

\(\begin{aligned} v = iR + L \frac{di}{dt} + \frac{Q}{C} &\qquad v = \frac{d\Phi}{dt} \\ i = \frac{v}{R} + C \frac{dv}{dt} + \frac{\Phi}{L} &\qquad i = \frac{dQ}{dt} \end{aligned}\)

This particular duality is especially important for me because I do research with superconducting electronics, where it’s often more convenient to describe circuits in terms of magnetic flux flow instead of current/voltage. For example, Josephson junctions⁠03 The subject of the 1973 Nobel Prize in Physics are weird devices that require a whole page of quantum mechanics to explain in terms of current/voltage. But when viewed in terms of magnetic flux flow, they’re essentially just switches – much easier to understand than quantum mechanics!

Duality is a gift that keeps on giving, and I hope we’ll see even more of it in the other bloggers’ posts this month.