Designing a Calculator with FSM Logic by Selam G. '18
A web dev lesson from an MIT sophomore!

My friend Robert V. ’20 is a Course 6-3 (Computer Science) sophomore, the MIT African Students’ Association’s webmaster, and has TA’d an interesting IAP class called 6.148, a web development class and competition. He’s a really smart guy, and I found out about this cool post he put up on Medium and asked if I could reformat it and post it to the blogs. Robert is passionate about web design and development, and is also really great at teaching. He’s always the first person that many of our Course 6 freshman friends reach out to for help in their introductory courses. Robert lives in Maseeh Hall, was born in Goma and grew up in Kinshasa in the Democratic Republic of the Congo. I hope you enjoy his post as much as I did!
As far as I can tell, making a calculator is a classic first time programmer’s challenge. So, as I was helping some of my fellow underclassmen learn web dev, I suggested making a calculator! For best practice purposes, I also suggested starting off with brainstorming:
- First, we design how this calculator is going to work,
- Then, we can implement code for this,
- And finally, we can make it pretty
As we were brainstorming, we naturally through that a coherent design logic for our calculator would be a finite state machine (FSM)!
WAIT. What’s a Finite State Machine (FSM)?
NOTE: If you’re familiar with FSMs, you can skip this section entirely.
An FSM is a mathematical objects made of states, state transitions, and inputs. FSMs are widely used in computer science and engineering to model the behaviors of machines. At any given time, an FSM has one state and can receive inputs. Based on those inputs, the FSM can change both state (through state transitions) and interval variables of the FSM.
HERE’S AN EXAMPLE: The state machine of the human body.
A very simplified human body has 2 states: hungry and full. When humans are hungry, they need food in order to get back to being in the full state, and at the same time, they may become happy when they get food. Becoming happy in this case would be an internal variable of the state machine, and eating would be an input.
Then, humans use all their energy (the other input) which makes them hungry again. They could become SAD too.
So, inputs essentially lead to state change in a state machine. Here’s what this simple human body state machine would look like when graphically represented:
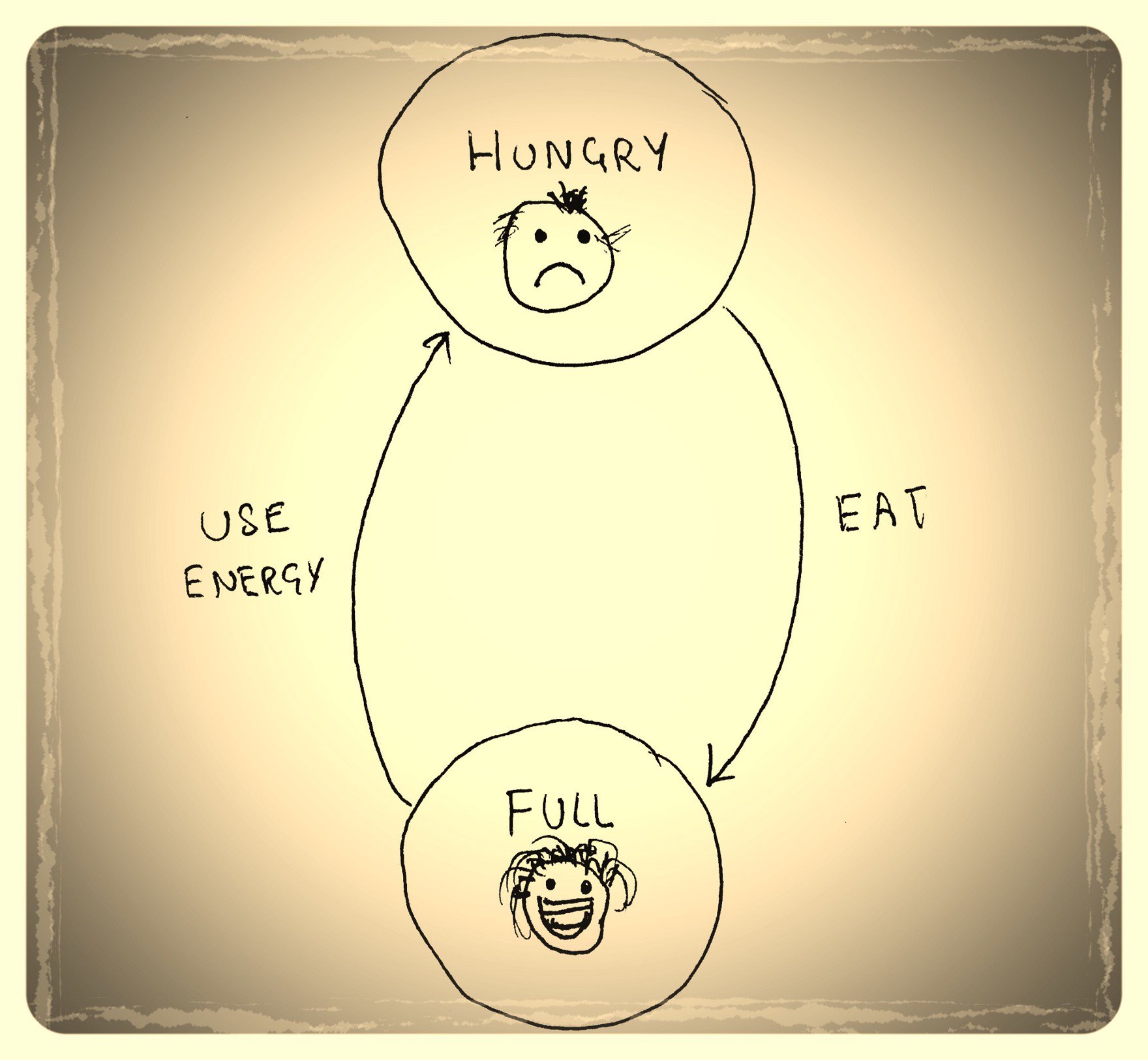
Ok, let me show you another example!
You’re about to see an FSM that you’re very familiar with but that was just never called an FSM: the state of matter.
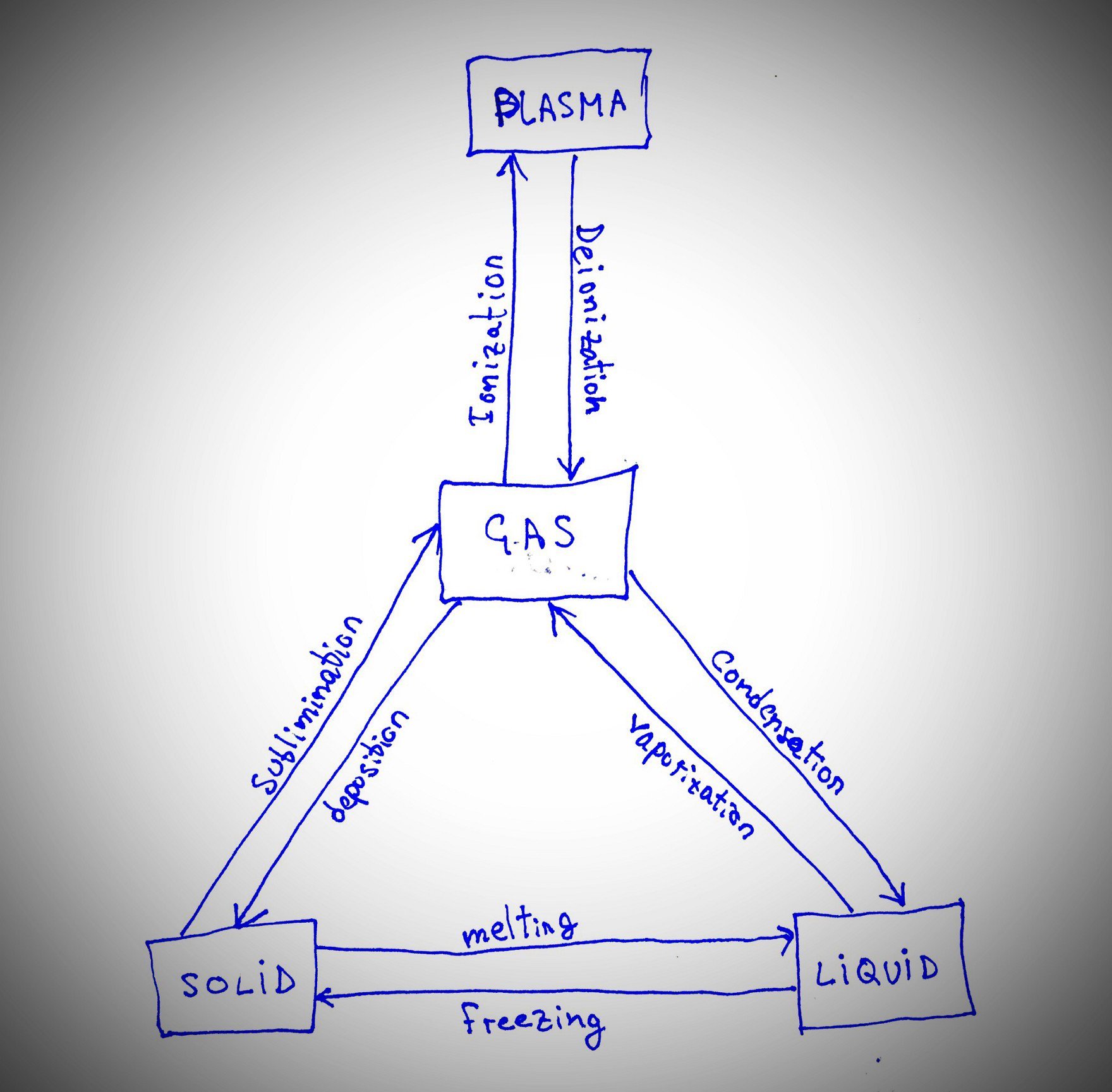
Right, isn’t that cool? We learn this in high school, but they never call it that way. Anyway, this state machine has 4 states: PLASMA, GAS, SOLID, LIQUID. There are transitions from states to states, which are inputs that are either caused by nature or by humans. Internal states of this state machines could be, for example, the boiling temperature of the given matter, the name of the given matter, etc.
Why Are (Finite) State Machines Important?
They provide us with a very systematic way of modelling anything that can happen in real life (such as state of matter). Based on state machines, we can easily use mathematics to derive both properties of those machines. State machines are widely used in probabilistic applications, such as modelling the motion of a robot looking for a reward located somewhere the robot does not know using Markov Random Process (which is also a subset of state machines). State machines also allow to naturally and easily expand our model (both through the design and through code). For example, in the human body, we could add another state, not full / not hungry, where the human person could be feeling meh. To add that, we simple create a new state and add some transitions to it.
Of course, there are times when other models are better, but state machines work best for certain kinds of applications.
Finally, if you’re more interested, here’s an article on embeddedrelated.com by Jason Sacks that goes over a lot more details that I did. If you find this interesting, you will love that article.
Back to Calculators
Later on, we decided to use the iPhone’s calculator to identify all the possible states in our calculator state machine simply by playing around doing multiple arithmetic computations. And…
It quickly turned out to be much more complicated than I thought.
Here’s some thought to not using a state machine:
- Designing a calculator without thinking about all the state machine’s logic is very simple. It works well for most operations, and noticing the imperfections in it can be subtle. However, there are operations that simply do not work well, such as 2 + 4 * 2, which in reality is 2 + (4 * 2) = 10 and can be erroneously evaluated as (2 + 4) * 2 = 12.
- Another way to design a calculator is one where the user can input expressions, such as 3 * 4, which can be easily evaluated with functions like eval. Not that I am not suggesting using eval (it’s know to be a bad practice); it’s just a quick solution that could help quickly get down to implementing all the UI for the calculator.
However, nicely designing a calculator with a correct finite state machine is not that easy. Nevertheless, I decided to pursue this interesting challenge, and this is what I came up with:
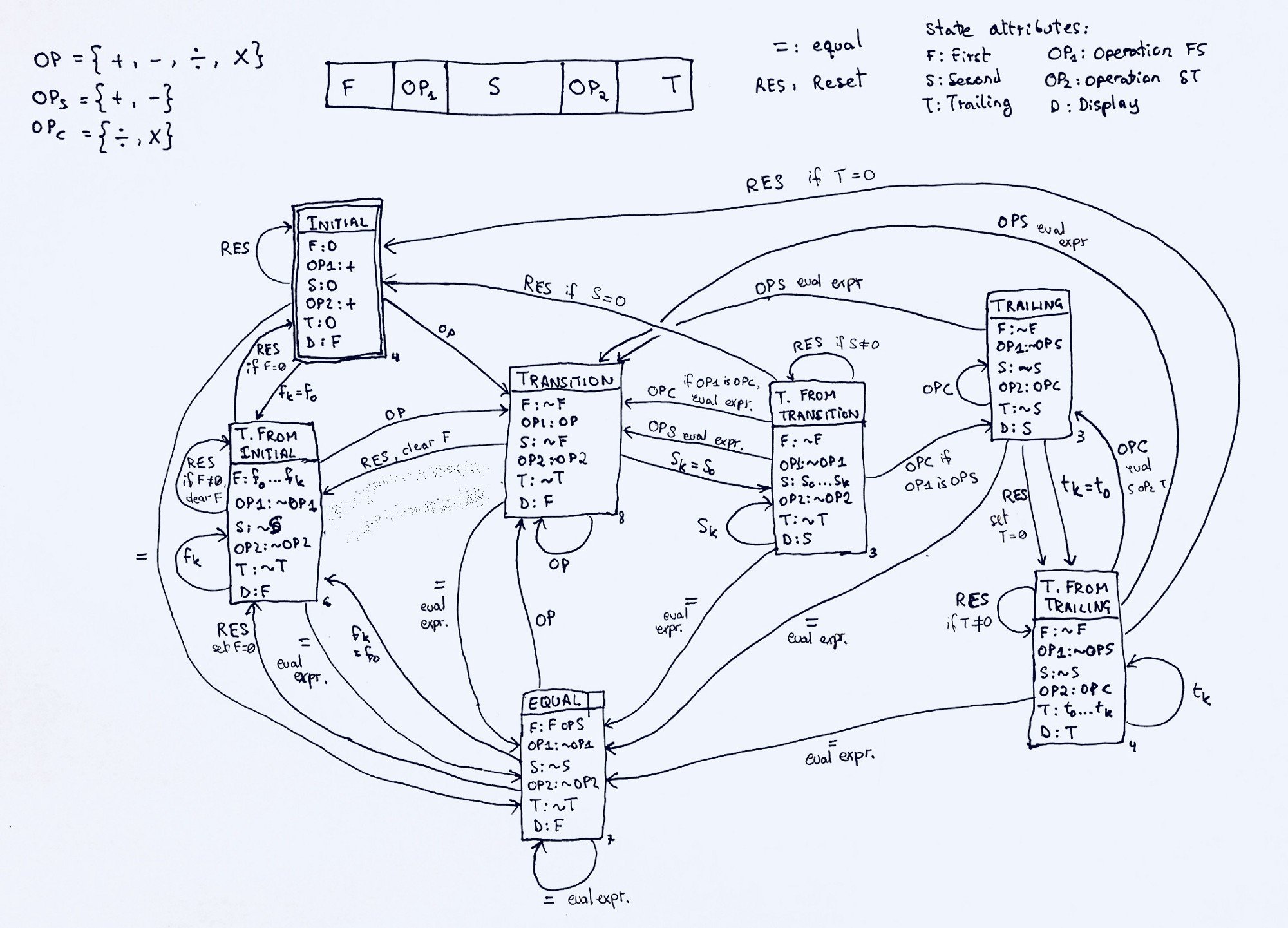
That looks quite complicated. Let me explain.
Note: if you’d like to skip to the end, I posted JavaScript gist code snippet that implements this.
The main idea behind a simple calculator is that we receive inputs, and based on those inputs, we make some operations, and if needed, we change the output display on the screen.
Inputs may be:
- numbers (one of 0,1,2,3,4,5,6,7,8,9,.. note that I included the . as a “number”),
- operations (one of +,-,*,/),
- equality (i.e. =), or
- reset (could be C or AC on iPhone. One of them is clear which is same as clear entry and the other is clear all).
Then, we can denote the inputs as follows:
- Operations are OP for +,-,*,/, OPS for +,-, and OPC for *,/. C for complex, S for simple.
- Equality is just =.
- Input numbers may be one of fk, sk, or tk. The “k” actually stands for the new input’s index for numbers such that a number is a sequence of digit characters f0,f1,f2,…,fk-1, and the input makes the number become f0,f1,…,fk. For example, in 123, f0=1, f1=2, f2=3 and k-1=2. The input f3=4 will change that number into 1234.
- The reset button is RES. This is like pressing AC or C on your iPhone’s calculator.
Next, I designed the underlying structure of the calculator as blocks of the form:
|---|-----|---|-----|---| | F | OP1 | S | OP2 | T | |---|-----|---|-----|---|
- F stands for “first” as in “first number”
- OP1 is the first operation
- S is stands for “second” as in “second number”
- OP2 is the second operation, and finally
- T stands for “trailing” as in “trailing number”.
By now, you can probably imagine that we’d be doing operations against the first and second number and against the second number against the trailing number, but how are the operations actually made, what do each of those blocks actually mean, and where does the result get stored? Let me explain all of it!
The State Logic
What we need is to identify all the possible states for this FSM. This is the difficult part. I learned here that this type of calculators try to make the most logical assumption while respecting the rules of mathematics, and it can be beautifully describes with only 7 states! Before diving into these 7 states, first, here’s what the state parameters in a state represent:
F <- the value of the first number OP1 <- the operation between the first and second number S <- the value of the second number OP2 <- the operation between the second number and trailing number T <- the value of the trailing number D <- what is displayed on the screen; it can be one of F, S, and T
The inputs that I listed above are what will lead to various state transitions. Now, onto the states:
STATE 1: INITIAL State
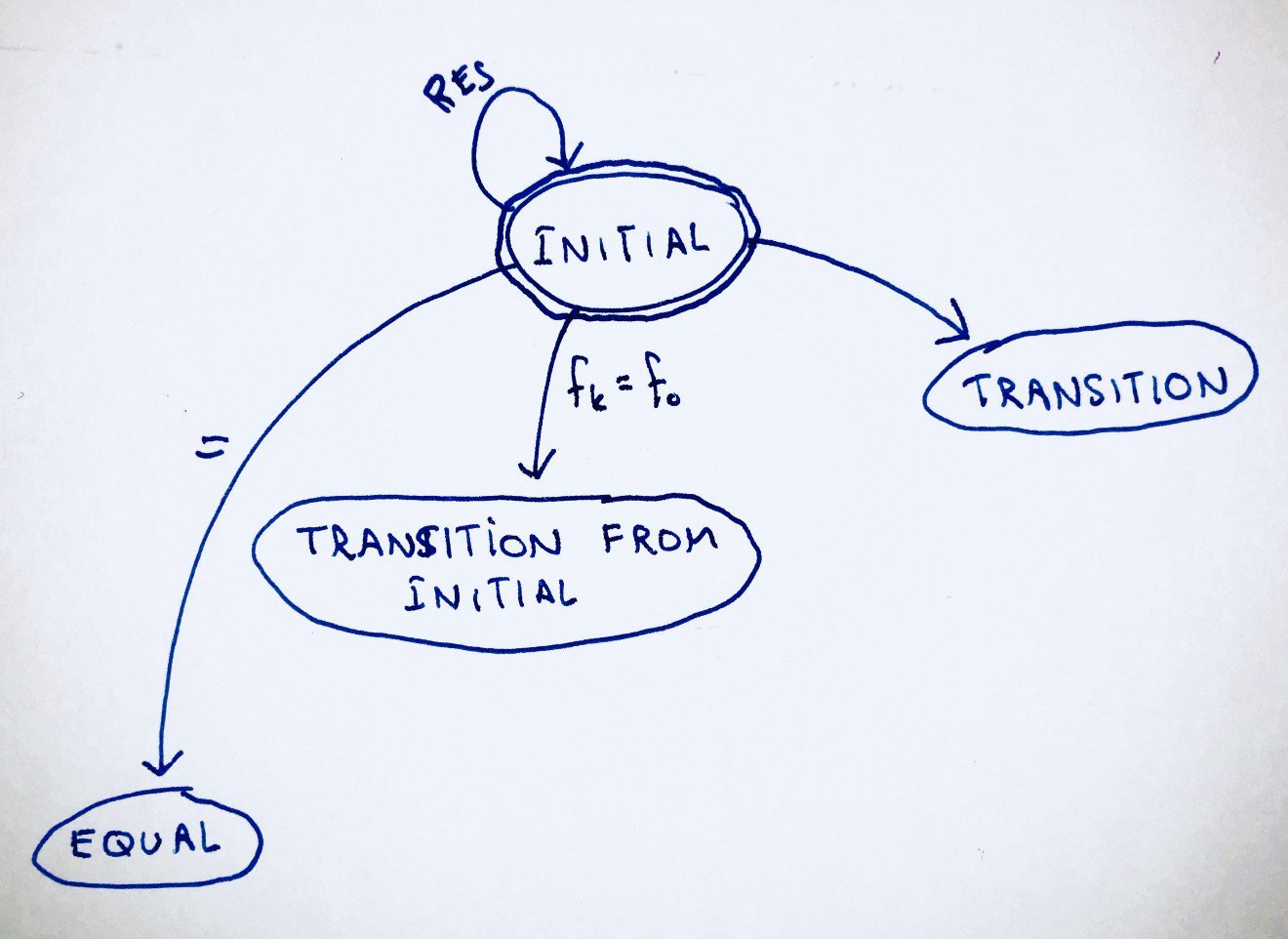
So, the initial state looks like:
F: 0 OP1: + S: 0 OP2: + T: 0 D: F
This is the state we start off with. There’s nothing interesting, and the values that we start with are just zeros and + operations.
Pressing RES will take us back to the initial state: it essentially has no effect. YES, self loops are allowed in FSMs.
Pressing any number, denoted by fk (which must be equal to f0 for this input coming from the INITIAL state) will take us to the TRANSITION FROM INITIAL state. I will talk about that state next. The number is denoted with lowercase f because it will be filled into the first number F. Note that adding numbers into other blocks will then have to either be sk or tk for block S and block T respectively.
Finally, pressing any operation OP will take us to the TRANSITION state. Note that this will change OP1 to become OP, whatever OP may be among +,-,*,/. This state is upcoming as well.
STATE 2: TRANSITION FROM INITIAL
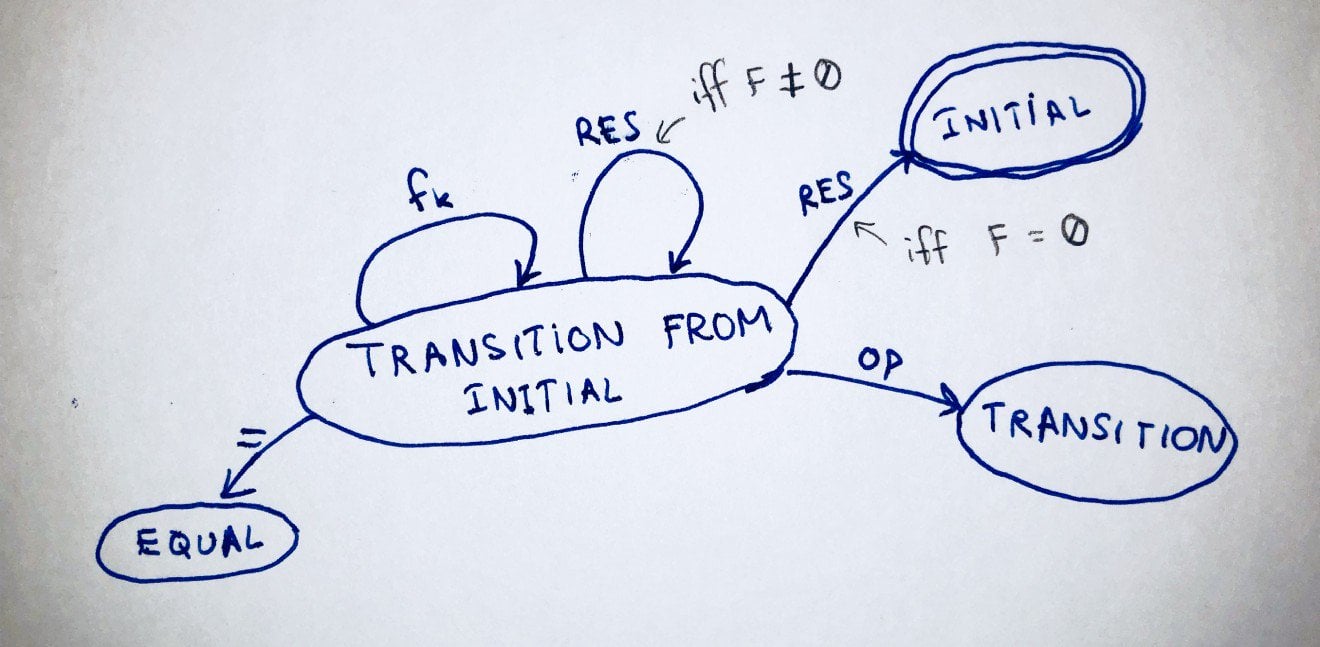
Let me point out that my naming convention here is a bit weird, but I tried my best to give these states meaningful names.
Without further ado, this state looks like this:
F: f0...fk-1 OP1: ~OP1 S: ~S OP2: ~OP2 T: ~T D: F
Some things to note: I use the ~ notation to denote that the value of this key is whatever the given state key was before (not that it could be that the state key does not match state key, e.g.: S: ~F). Some later states will cause these values to change and not be + or 0 as in the initial state.
So, anyway:
Pressing RES will take us to TRANSITION FROM INITIAL state (i.e. back to here) if F is not equal to 0. It will clear F (i.e. set it to 0). Pressing RES will take us back to INITIAL state if F = 0. This means all parameters become what they used to be. i.e. F=0, OP1=+, S=0, D=F, OP2=+, T=0. I will show why this is important at the end.
Pressing any number fk will take us back to this same state, TRANSITION FROM INITIAL and simply append fk to f0…fk-1.
Pressing the = sign will take us to the EQUAL state. Through this, it will make the evaluation (F) OP1 (S) and place the result in the F block when it reaches the equal state.
Finally, pressing any operation OP will take us to the TRANSITION state. Note that this will change OP1 to become OP, whatever OP may be among +,-,*,/. This will also duplicate F into S.
STATE 3: TRANSITION
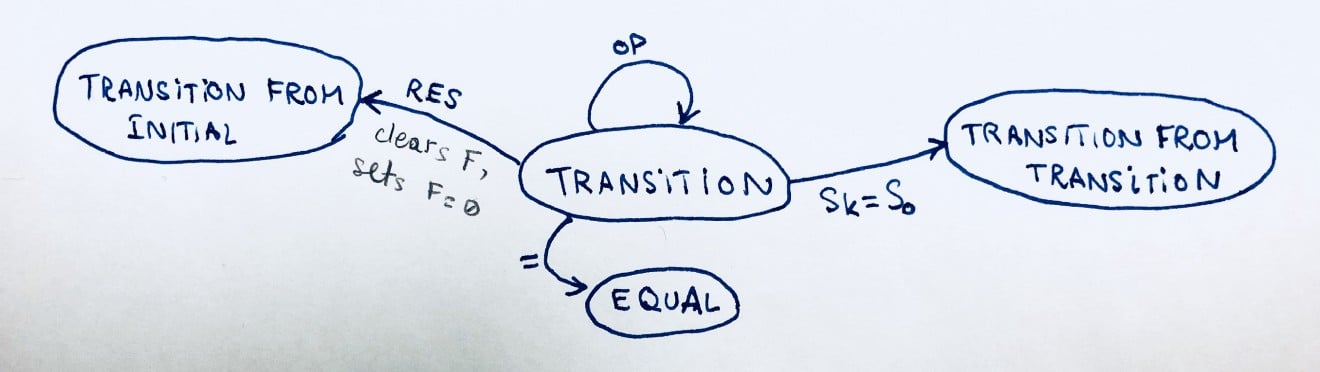
If you go back to the visual, you will notice that this state is the most frequented state (i.e. has the most arrows coming into it). EQUAL is the second most frequented.
Anyway, this state looks like:
F: ~F OP1: OP S: ~F OP2: ~OP2 T: ~T D: F
Note that to reach this state, one must press an operation OP; that is the value that OP1 takes! There’s also something funny that happens here: the value of F gets duplicated into S. This is an optimization that was made by the iPhone. It’s a design decision that did not have to happen but works very well. Let’s say you press 3 then *. Then, what happens if you press = ? Do you get a zero because you didn’t type the second number? With this design decision, you’d get a 9 because we assume that you meant 3 * 3. I think it’s cool that they thought of this!
Then, pressing any OP leads us back to this state. It simply changes the operation to the new one.
Pressing = evaluates (F) OP1 (S) and places the result in F. Then, it takes us to the EQUAL state. Note that when it takes us to the equal state, both OP and S and every other parameters of the state remain unchanged. This is also cool. Do you see why? Maybe it’ll be more obvious once we get into the EQUAL state.
Pressing RES takes us back to TRANSITION FROM INITIAL. On the way to it, it removes all the values in F and replaces it with 0. All the other parameters remain unchanged.
Finally, pressing another number sk takes us to the TRANSITION FROM TRANSITION state. As you can imagine, this changes the value of S. Note that as coming from TRANSITION, sk = s0 (the very first index of the second number regardless of what S currently is, it will overwrite it).
STATE 4: TRANSITION FROM TRANSITION
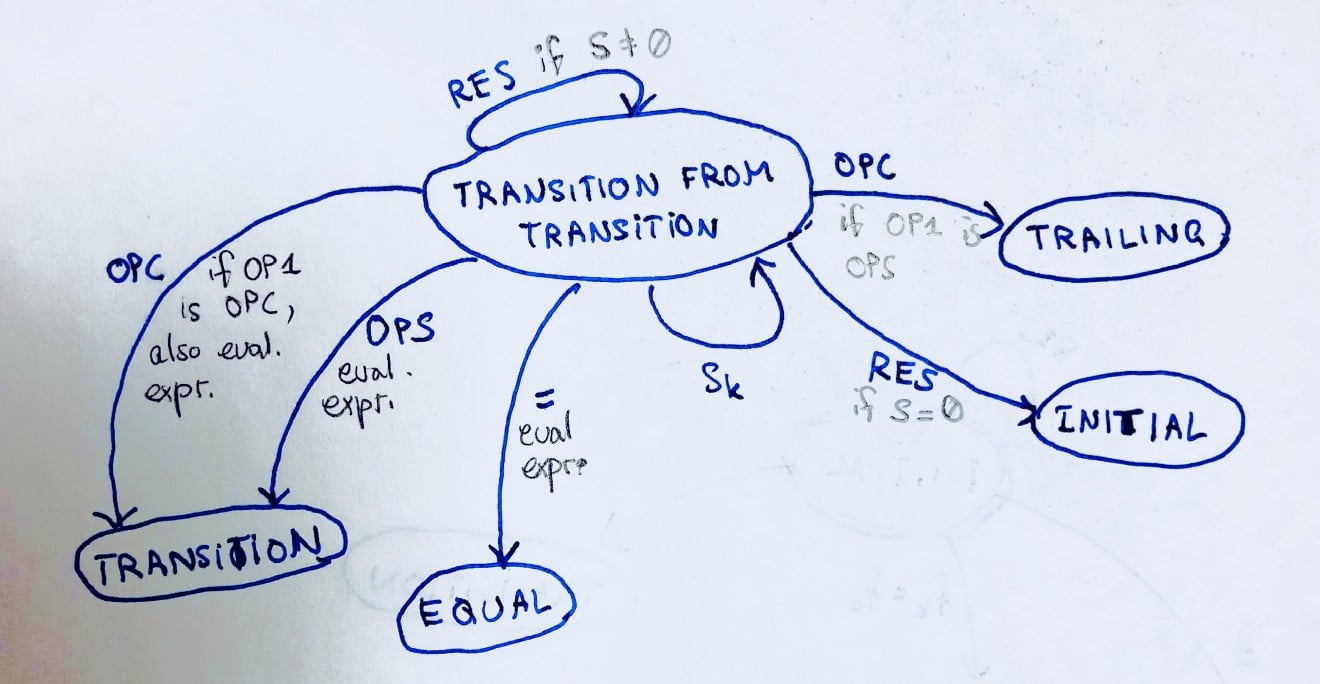
(That naming though… Sigh)
This state is interesting. It looks like this:
F: ~F OP1: ~OP1 S: s0...sk-1 OP2: ~OP2 T: ~T D: S
You can probably note that the display has now changed from F to S. Now, we’re displaying the second number!
Pressing sk takes us back to this same state, it just appends sk to S so that it now becomes s0…sk.
Pressing = takes us to the EQUAL state. Again, it will evaluate (F) OP1 (S) and place the result in F and also keep all other parameters unchanged.
Pressing RES takes us back to TRANSITION FROM TRANSITION if S is not equal to 0. This will clear S and replaces it with 0.
Pressing RES when S = 0 will take us back to INITIAL. This means that everything will get back to what it started off with.
Finally, pressing OP is the interesting case. There is actually two possible cases here:
- If we press OPS, we evaluate the expression (F) OP1 (S) and place its result on F. It will also place that same result on S as well. This is because we’re doing a simple + or – operation, so we can just evaluate the pression. OP1 will become OPS, whatever it may be. Then, it will take us back to the TRANSITION state.
- If we press OPC and OP1 = OPC, then we do the same as when we press OPS except it’s OPC. of course.
- Finally, if we press OPC, we will be taken to the TRAILING state if OP1 is OPS (i.e. if OP1 is one of + or –). In this state, OP2 becomes OPC (i.e. one of * or /) and OP1 is always an OPS. S remains what it was, which is s0…sk-1, but T will now get the value of S. The display D and S remain unchanged.
STATE 5: TRAILING
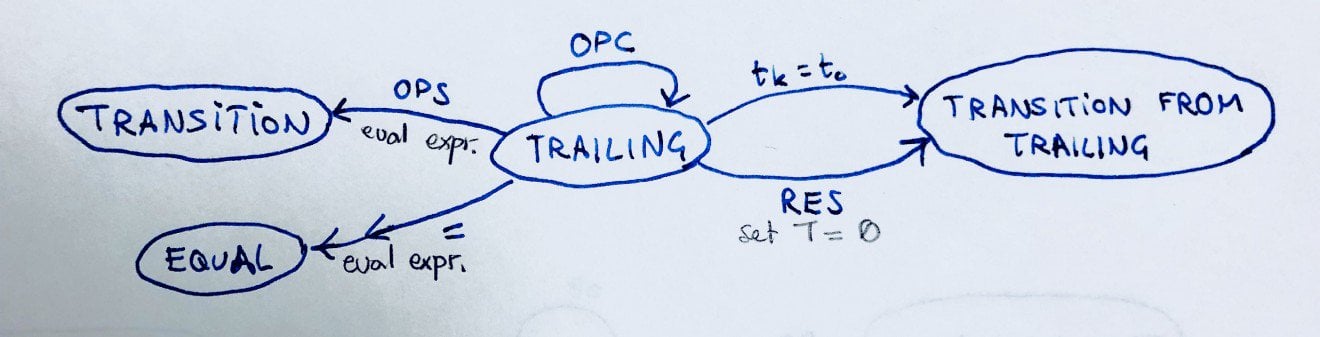
Why do we have a trailing state?
Imagine the expression 9+5*2, should it evaluate to 14*2=28 or should it evaluate to 9+10=19? If you care about Mathematics, you know that multiplication takes precedence. That is why we have both the TRAILING state and the TRANSITION FROM TRAILING state!
Note that in this state, OP1 is always OPS and OP2 is always OPC.
The TRAILING state looks like:
F: ~F OP1: ~OP1=OPC S: ~S OP2: OPC T: ~S D: S
Pressing = takes us to the EQUAL state. The evaluation is different however. First, we evaluate (S) OP2 (T), place the result into S (note that we make this evaluation before moving to the equal state), then we evaluate (F) OP1 (S), which places the result into F (note that we make this evaluation after moving into the equal state). So, now, F is essentially (F) OP1 ((S) OP2 (T)). All other expressions remain unchanged.
Pressing RES will take us to the TRANSITION FROM TRAILING state. This will immediately set T = 0 and all parameters will remain unchanged. The display will become T. Someone pressing tk = t0 is essentially equivalent to pressing RES from the TRAILING state.
Pressing OPC leads us back to the TRAILING state and simply change the OPC on OP2.
Pressing OPS will run the same evaluation done with pressing =, i.e. it will place (F) OP1 ((S) OP2 (T)) into F but also on place it on S. OP1 will be OPS, whatever it may be, and the display will be F. Other keys will remain unchanged.
Finally, pressing tk will take us to the TRANSITION FROM TRAILING state. In this case (i.e. coming from TRAILING), tk = t0. The display also changes to D=T .
STATE 6: TRANSITION FROM TRAILING
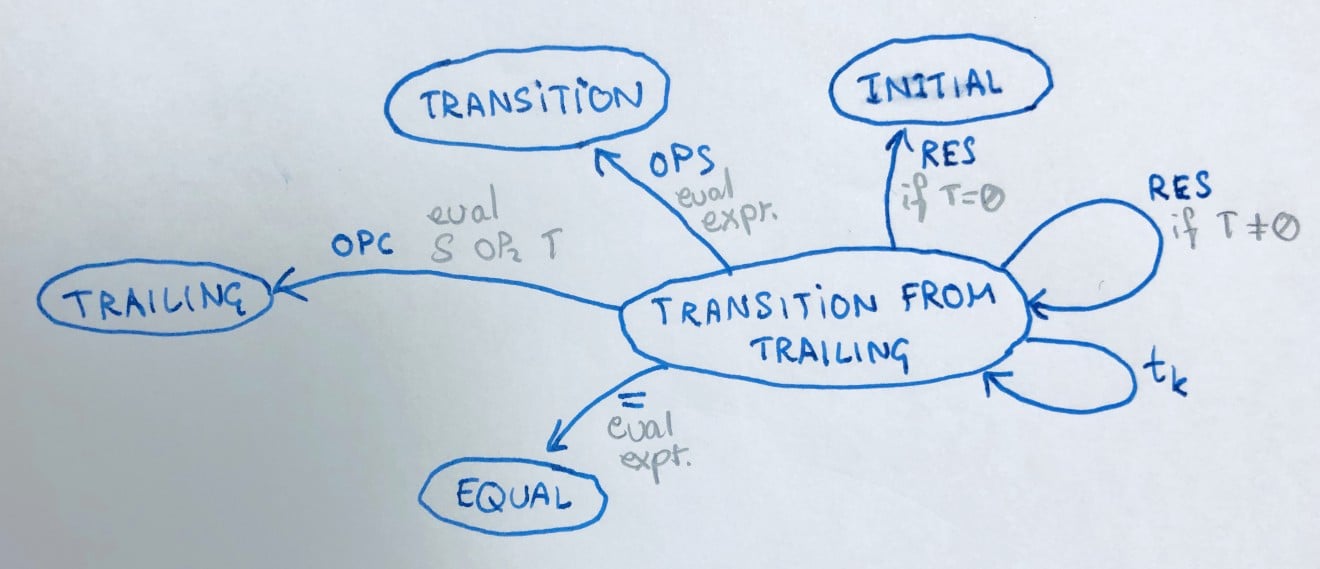
This state looks like:
F: ~F OP1: ~OPS S: ~S OP2: ~OPC T: t0...tk-1 D: T
Pressing RES if T = 0 will take us back to INITIAL state. Everything will be cleared. However, if T is not equal to 0, pressing RES will just clear T (i.e. set it to 0) and remain in this state.
Pressing tk will just append tk into the current value of T.
Pressing = will evaluate the expression just as evaluated when pressing = during the TRAILING state, and it will take us to the EQUAL state.
Pressing OPC will take us to the TRAILING state. This will evaluate (S) OP2 (T) and place the result in both S and T. Then, it will change OP2 to be the new input OPC . The display will change back to S.
Pressing OPS will take us to the TRANSITION state. This will evaluate the expression similar to how it’s evaluated in the TRAILING state.
STATE 7: EQUAL
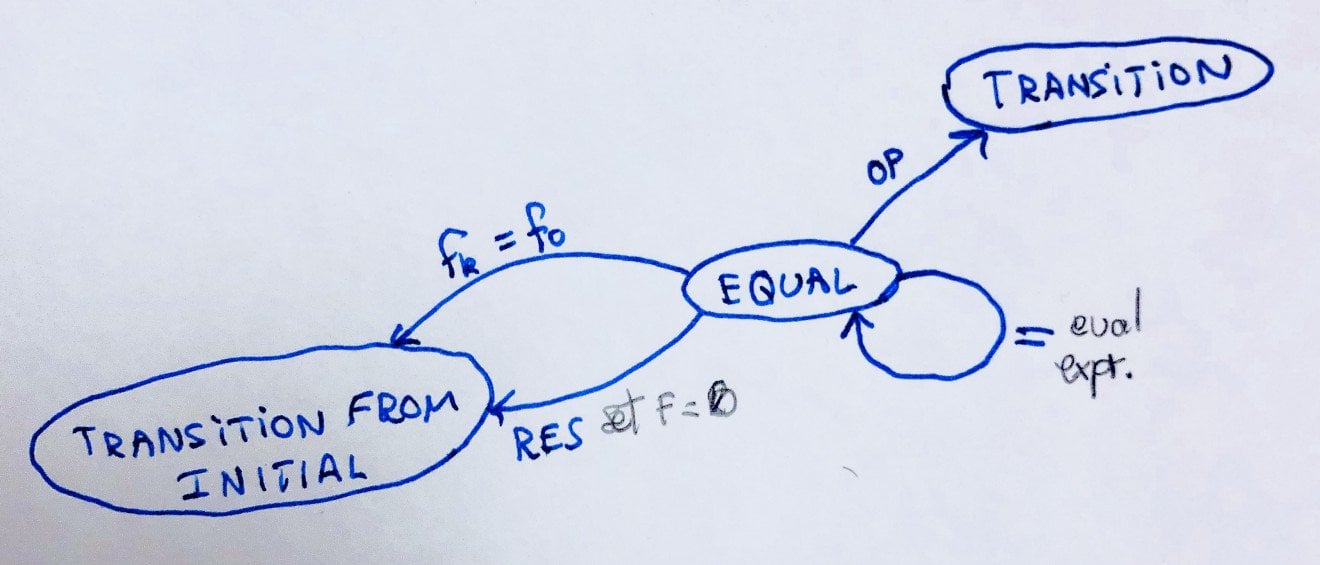
Whew! Finally, the EQUAL state. This state looks like:
F: (F) OP1 (S) OP1: ~OP1 S: ~S OP2: ~OP2 T: ~T D: F
Note that the display in the equal state is always F.
Pressing = re-evaluates (F) OP1 (S) and places the result into F. Note that S will remain the same in this case.
Pressing OP will take us to the TRANSITION state. Then, it will make a copy of F and place it into S. Then, OP1 will be the newly received operation.
Pressing fk will take us to the TRANSITION FROM INITIAL state. In this case, fk = f0. Everything else will remain unchanged.
Pressing RES will also take us back to the TRANSITION FROM INITIAL state. However, it will delete F and replace it with 0.
The Calculator (an example!)
Parting Notes
This is the calculator shown in the video above. It’s a really nice state machine that works well for these simple operations, and the design is great because it can be easily expanded to more complicated operations such as sin or floor.
I wanted to point out that I didn’t really talk about how we are appending to the numbers. In case fk (or equivalently sk and tk ) is . , we only append when there is no . in the number. For example, pressing . when F=243 will make F=243. . However, pressing . when F=23.5 will have no effects! Also, pressing any number other than 0 when F=0 needs to change F into that number (equivalently for S and T).
This is definitely not crazy difficult, but I’d say it’s more complicated that it looks, and it’s been a rewarding exercise to actually design this calculator. Here’s code that I wrote that does this in JavaScript (which is meant to be used for a calculator website)