
What is a zonotope? by CJ Q. '23
yes this is a post about math
What is a zonotope? Get a sheet of paper and draw some vectors in the plane, no two of which are parallel. I picked four vectors. In this picture, I drew them all originating from a single point, and with different colors:01 What do these colors remind you of? Google? The MBTA? Microsoft?
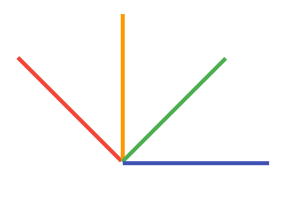
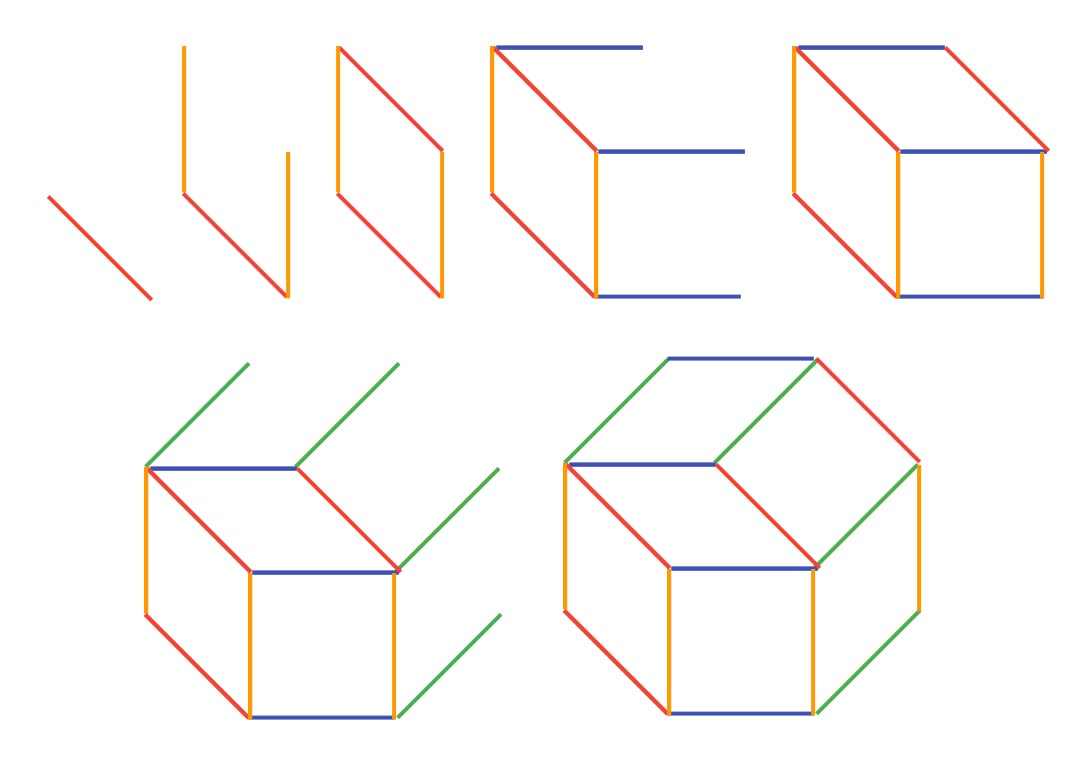
Pick some ordering of your vectors. Here, we’ll go with the order red, orange, green, blue.
Draw the first vector, somewhere, making a line segment. Then draw the second vector originating from each end of the first segment. Connecting these two ends should make a parallelogram:

Now repeat this process with the next vector. From each vertex of the parallelogram, draw the third vector if it won’t intersect with it. In my example, I’ll draw the third vector on every vertex except the lower-left one. (If I drew it starting from the lower-left one, it would be “inside” the parallelogram, which we don’t want.) Then connect these endpoints to form a hexagon.
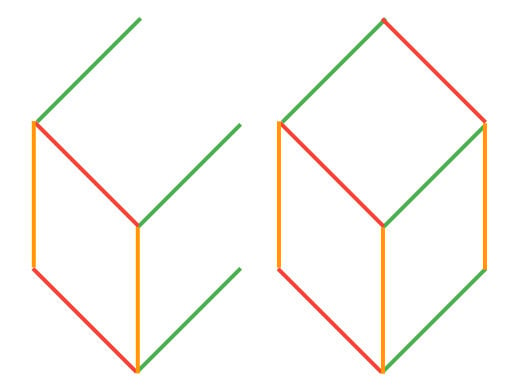 Repeat the process. Draw the next vector on each vertex if it’ll be “outside”, then connect it. I only have four vectors, so this next step will be my last one; though you can keep doing this until you’ve used up all your vectors.
Repeat the process. Draw the next vector on each vertex if it’ll be “outside”, then connect it. I only have four vectors, so this next step will be my last one; though you can keep doing this until you’ve used up all your vectors.
 The boundary of your shape, at the end of this process, is called a zonotope. In our case, zonotopes are polygons that have an even number of sides, and have rotational symmetry. You can rotate them 180° about the central point and you’ll get the same shape.
The boundary of your shape, at the end of this process, is called a zonotope. In our case, zonotopes are polygons that have an even number of sides, and have rotational symmetry. You can rotate them 180° about the central point and you’ll get the same shape.
During the process of drawing the zonotope, we’ve also made a (fine) zonotopal02 My spellcheck thinks zonotope is a word, but wants to correct zonotopal to Zootopia. tiling—a way to dissect the zonotope into pieces, each of which are a zonotope themselves. Notice how, when I drew the edges in this example, I made sure to use the color of the corresponding vector. Here’s a somewhat surprising fact. If you pick any pair of original vectors, like red and blue, then there’s exactly one tile that has those vectors as sides:
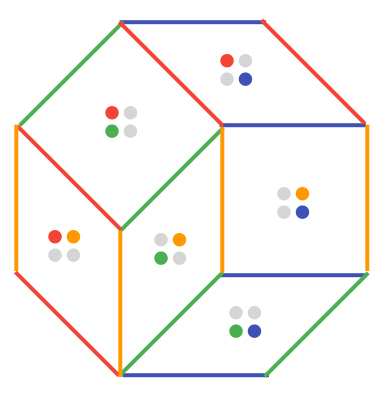 And this is true no matter how you drew the vectors you picked for your zonotope, or which order you chose to draw them in! So without even drawing the zonotope, we already know how many tiles there will be; it’s the same as the number of pairs of vectors. Can you come up with an explanation why?
And this is true no matter how you drew the vectors you picked for your zonotope, or which order you chose to draw them in! So without even drawing the zonotope, we already know how many tiles there will be; it’s the same as the number of pairs of vectors. Can you come up with an explanation why?
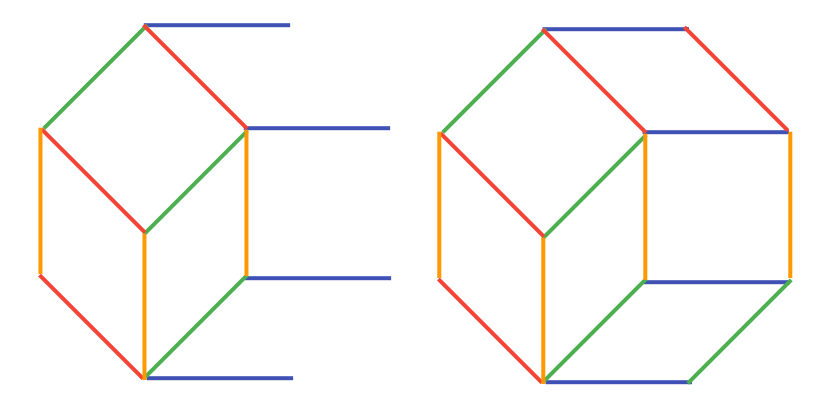
Zonotopes and wires. Here’s the reason they’re called zonotopes. Starting from the lower-left segment, which is red, we can draw a line03 a curved line, which is a line,,, okay,,, connecting all the red segments, which goes all the way to the opposite side. We can do something similar for each vector, giving us this picture:
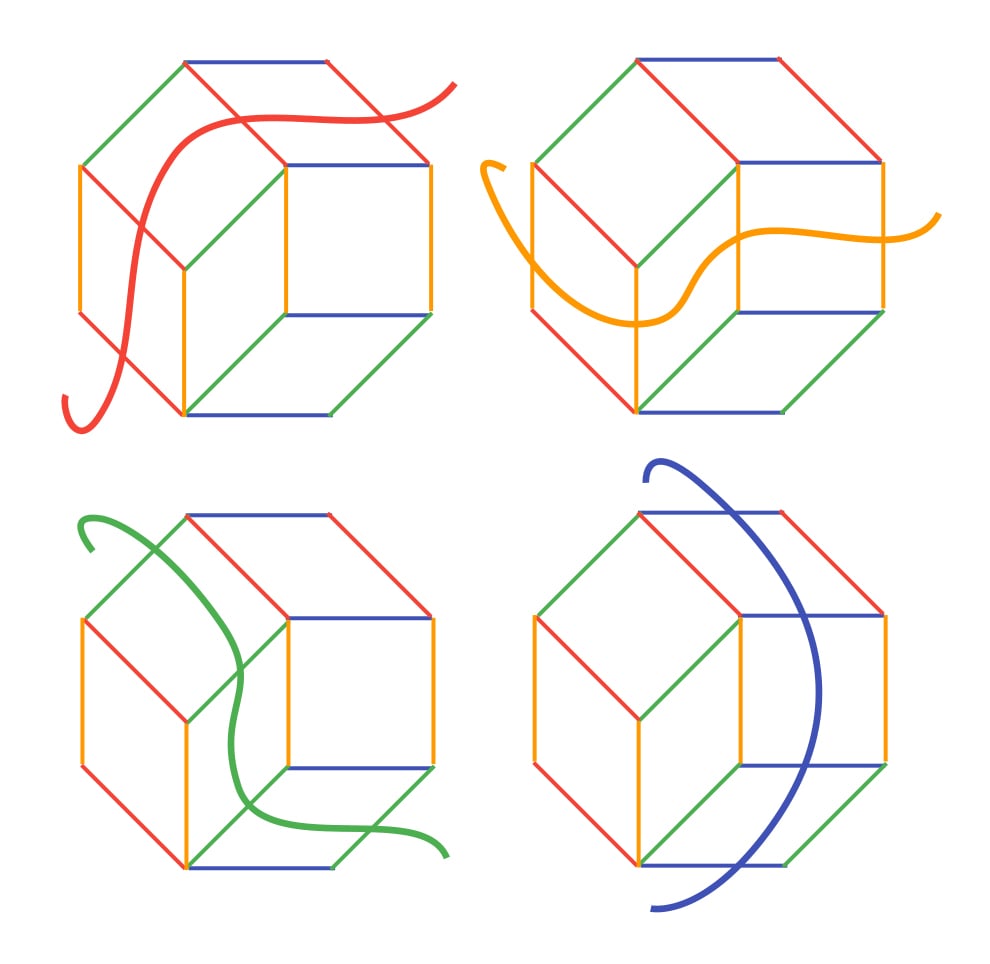 So the tiles with a certain vector as a side all line up, going from one end of the zonotope to the other end. It’s like a belt which wraps around the shape, which is where we get the name zonotope, with zona meaning belt in Latin. The fact that they form a belt is also pretty cool.
So the tiles with a certain vector as a side all line up, going from one end of the zonotope to the other end. It’s like a belt which wraps around the shape, which is where we get the name zonotope, with zona meaning belt in Latin. The fact that they form a belt is also pretty cool.
Here’s an explanation of why this is possible. When you draw a line from one end of a parallelogram to the other end, you’re going from a side to a side that’s parallel. And because there are only a limited number of parallelograms, eventually you’re going to draw out of the zonotope. What this doesn’t explain, though, is why this line should go through all the parallel vectors inside, and that’s something I’ll leave for you to think about.
Let’s draw all these lines on top of each other: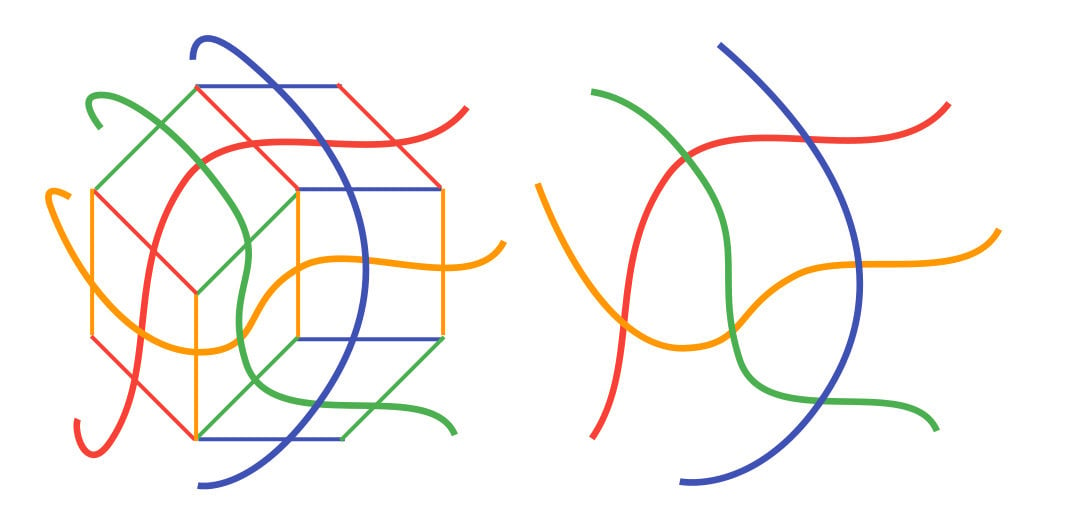 Notice that when we read the colors of the edges around the zonotope, we get the order red, orange, green, blue, and then red, orange, green, blue again. This is because the zonotope has rotational symmetry. Remember that if we rotate it 180° about its center, we get the same shape. This is why you should get the same order again.
Notice that when we read the colors of the edges around the zonotope, we get the order red, orange, green, blue, and then red, orange, green, blue again. This is because the zonotope has rotational symmetry. Remember that if we rotate it 180° about its center, we get the same shape. This is why you should get the same order again.
Now look at the right diagram, where we draw just the lines, removing the zonotope. Read the colors of the “left side” from top to bottom: it’s blue, green, orange, red. Then read the colors of the “right side” from top to bottom: it’s red, orange, green, blue. They’re in reverse order.
We can stretch out the lines a bit, making the “left side” and the “right side” clearer, while still preserving the intersections between the lines:
 It takes a bit of looking back and forth to see why this is “essentially” the same drawing, but this represents more clearly what we have. We have a way that turns a series of wires into the reverse order, where we only swap two adjacent wires at a time.
It takes a bit of looking back and forth to see why this is “essentially” the same drawing, but this represents more clearly what we have. We have a way that turns a series of wires into the reverse order, where we only swap two adjacent wires at a time.
Let’s do another example. We’ll use the same vectors, except we’ll add them in a different order. Previously, we did red, orange, green, blue. Now, let’s do red, orange, blue, green:
 Then we repeat the same process of drawing all the lines, and making the “wiring diagram”:
Then we repeat the same process of drawing all the lines, and making the “wiring diagram”: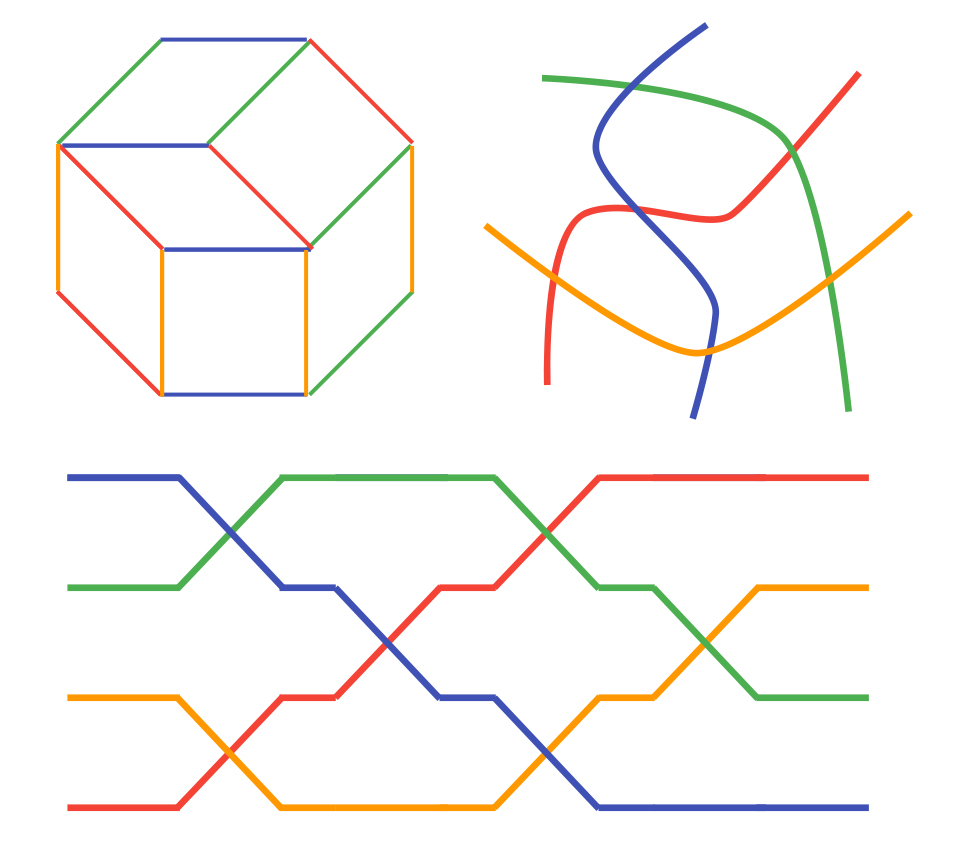 We then get a completely different wiring diagram. There are some similarities with the previous one. There’s the same thing with the wires starting in one order on the left, and then being reversed on the right. There’s also the same number of swaps, and they both have one swap for each pair of colors. (Why?)
We then get a completely different wiring diagram. There are some similarities with the previous one. There’s the same thing with the wires starting in one order on the left, and then being reversed on the right. There’s also the same number of swaps, and they both have one swap for each pair of colors. (Why?)
This leads to an interesting question. If we have two different zonotopal tilings, do they produce different wiring diagrams? And if we draw a wiring diagram, is there a zonotopal tiling that corresponds to it?
Three dimensions. Nice things about zonotopes also happen when we consider them in more dimensions. We can repeat our construction with three-dimensional vectors rather than two-dimensional ones. It’s a bit harder to visualize, but here’s an example:
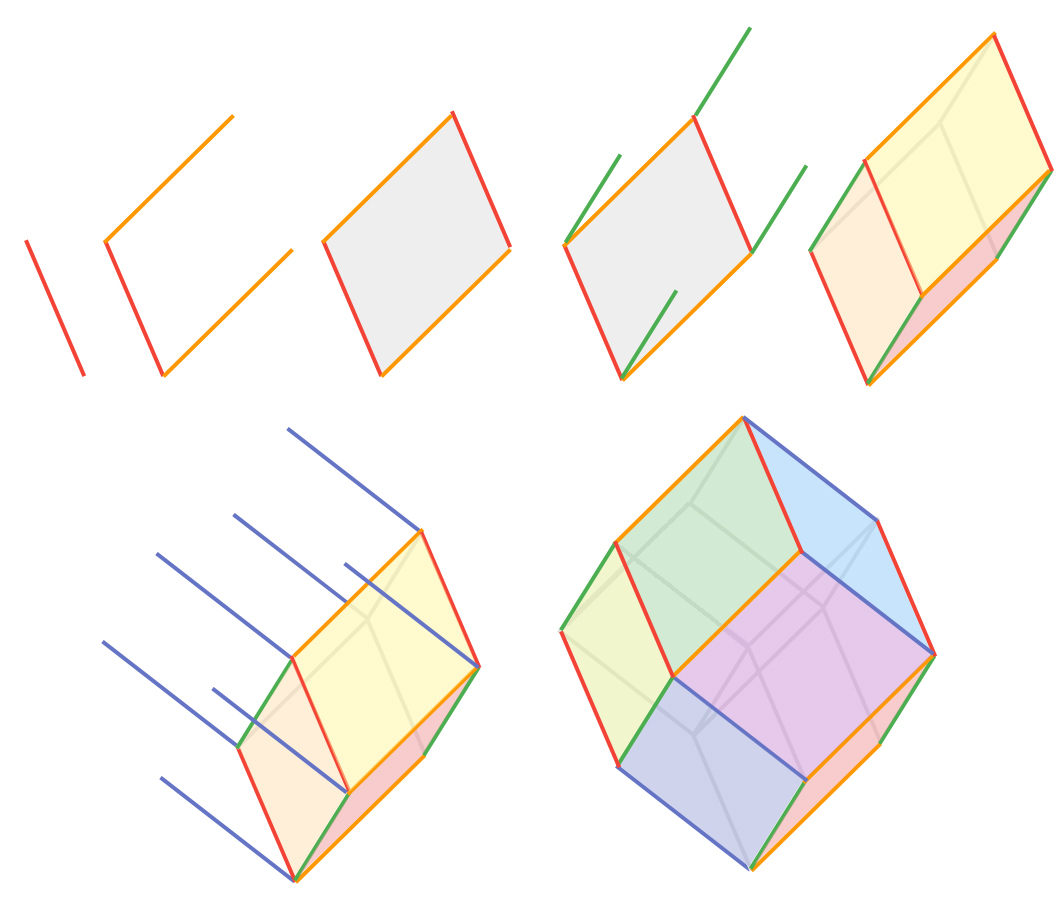
This is a dodecahedron with sides as parallelograms. Like a two-dimensional zonotope, it’s symmetric about its center. Here, if we focus on the faces that have a certain vector as an edge, the belts become even more evident:
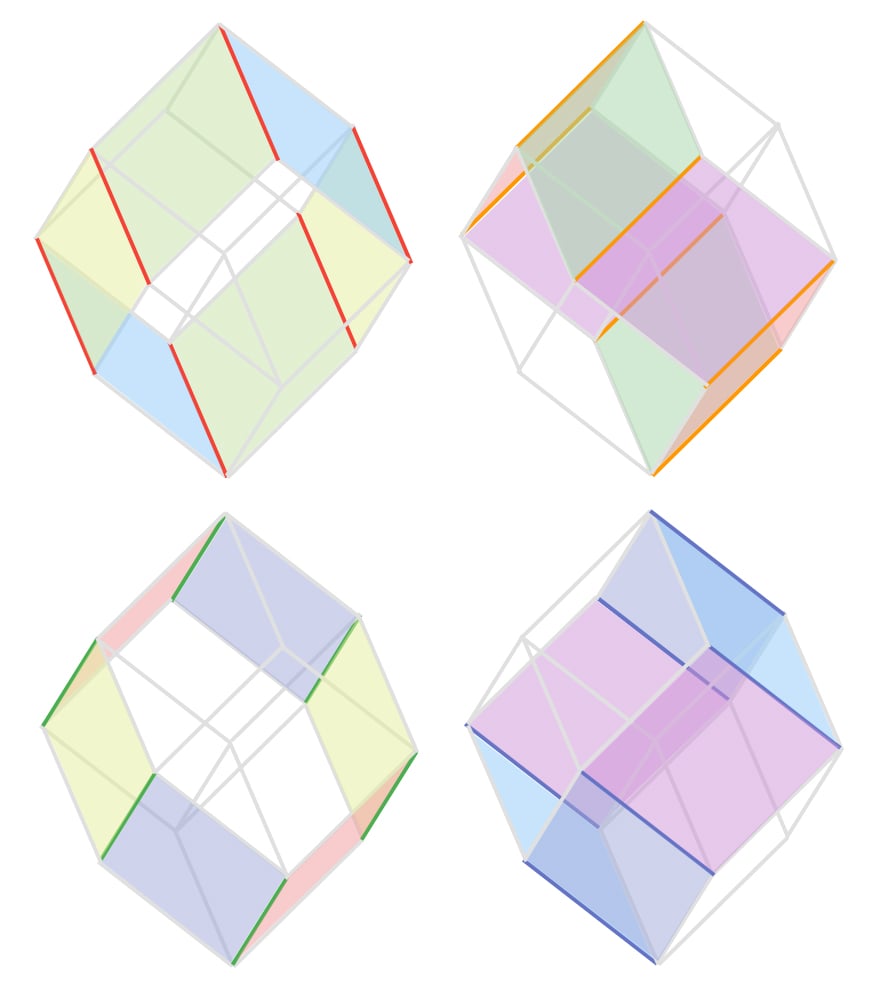
Because of the central symmetry, we still have opposite sides being the same. For example, we have two parallelograms with orange and green edges directly opposite each other, on the surface of the zonotope. We can count twelve different faces, making it a sort of rhombic dodecahedron.04 The Wikipedia page also has this <a href="https://en.wikipedia.org/wiki/File:R1-cube.gif">really pretty animation</a>.
Let’s consider the tiling itself, and ask the same questions. Is it still true that every pair of vectors give a unique parallelogram? Not really, but we have the next best thing: every pair of vectors gives exactly three parallelograms inside our tiling. (But why three? Does this change if we add more vectors?)
Let’s look at the tiles. Each of the tiles is again a zonotope; in this case, it’s a parallelepiped.05 I learned that this is pronounced pa-ruh-leh-luh-PAI-ped, and not pa-ruh-LEH-luh-paipd. I have been wrong forever. How many tiles are there? We can count four different tiles in the tiling:
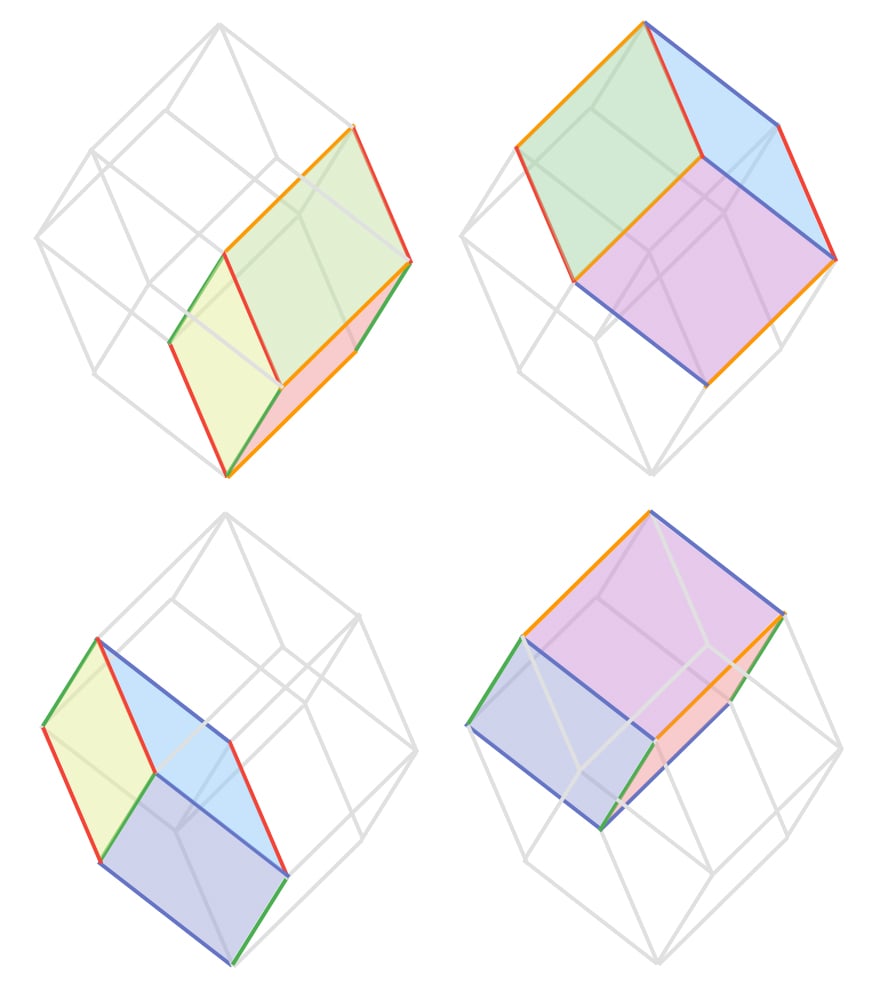 Now, we see that the tiles correspond to triplets of the vectors, rather than pairs. This makes sense: pairs of vectors in 2D, triplets of vectors in 3D. And also, each triplet of vectors corresponds to its own parallelepiped again. So there are four triplets of vectors, and four tiles. It’s harder to draw, but if we drew a 3D zonotope out of five vectors, there would be 10 tiles corresponding to 10 triplets of vectors, as long as the vectors aren’t bad.
Now, we see that the tiles correspond to triplets of the vectors, rather than pairs. This makes sense: pairs of vectors in 2D, triplets of vectors in 3D. And also, each triplet of vectors corresponds to its own parallelepiped again. So there are four triplets of vectors, and four tiles. It’s harder to draw, but if we drew a 3D zonotope out of five vectors, there would be 10 tiles corresponding to 10 triplets of vectors, as long as the vectors aren’t bad.
Vertices in zonotopal tilings. In which ways can the vectors end up being bad? Well, it can happen if a triplet of vectors don’t make a parallelepiped, or if the parallelepiped ends up being “flat”, like a sheet of paper rather than a box. These three vectors, for example, wouldn’t make a parallelepiped:
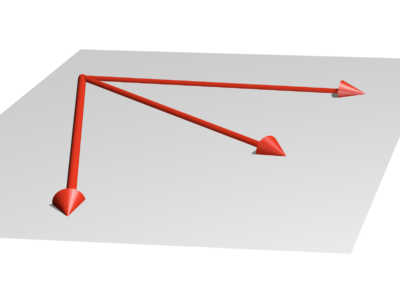
by schnelliboy, cc-by-sa 4
We call these three vectors linearly dependent. In other words, a triplet of vectors is linearly dependent if the parallelepiped they make is “flat”. Similarly, we can call a pair of vectors linearly dependent if the parallelogram they make is “flat”, which can happen if the two vectors point in the same direction. We call a set of vectors linearly independent if they aren’t linearly dependent.
I’m going to end the math with one last neat fact. The number of vertices in our zonotopal tilings is the same as the number of sets of vectors that are linearly independent! Here’s an example. Recall our four vectors from earlier:

First, each pair of vectors is linearly independent, which gives 6 sets. Each vector alone is also linearly independent, giving 4 more sets. Finally, the empty set is also linearly independent (trust me on this one), giving 1 last set. Triplets of vectors can’t be linearly independent, because they parallelepiped they make would be “flat”. In total, we have 11 sets. And how many vertices are in our tiling?
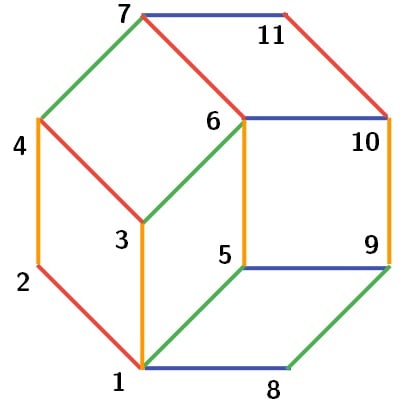 There are 11! And you’ll see that in the other tiling, there are also 11.
There are 11! And you’ll see that in the other tiling, there are also 11.
In the three-dimensional case, all 4 triplets of vectors, all 6 pairs, all 4 vectors, and the 1 empty set are all linearly independent, giving a total of 15 sets. And you can check that there are also 15 vertices in the three-dimensional example we have.
Now the big question is: why is this true? Why is this true for every single zonotopal tiling? What are the corresponding results in four dimensions, five dimensions, more? What is the business with the wiring diagrams going on earlier, and is there a way to do something similar in three dimensions?
These are the kinds of things we’re learning in 18.218, Topics in Combinatorics, which is one the classes I’m taking this semester. 18.218 is a topics class, which means that what it’s about changes yearly, depending on who’s teaching.
Professor Postnikov is teaching this year’s class on polytopes and hyperplane arrangements, and we covered questions like the above and more. I find this kind of math really interesting. Part of it is because it’s the kind of math you can draw and show people. The prerequisites are also pretty minimal, which is really nice, because you don’t need a lot of background to study it. Professor Postnikov is also a great lecturer too.
Alright, that’s it. Conclusions are hard.
- What do these colors remind you of? Google? The MBTA? Microsoft? back to text ↑
- My spellcheck thinks zonotope is a word, but wants to correct zonotopal to Zootopia. back to text ↑
- a curved line, which is a line,,, okay,,, back to text ↑
- The Wikipedia page also has this really pretty animation. back to text ↑
- I learned that this is pronounced pa-ruh-leh-luh-PAI-ped, and not pa-ruh-LEH-luh-paipd. I have been wrong forever. back to text ↑