Little Rectangles by Taylor V. '19

How smart am I?

I feel like I’ve asked myself this question a thousand times since I’ve arrived at MIT, but it’s never phrased exactly like that. “How can I be so stupid?” is common. “Why can’t I get this? Everyone else can”, makes an appearance. Or maybe the fun one, “Why do I even try?”.

I wouldn’t consider myself much of a sharer. On the blogs I mostly like to talk about MIT as a physical entity. “Look at this cool thing MIT did”, or “This is what MIT looks like”. This is not that blog. I’ve been marinating this post all semester, so it’s always sort of been at the back of my mind. It started as snippits and sentences that came to me when I was walking to class or sorting books in the library. Then I began adding larger chunks and incoherent paragraphs over the past few weeks. And now here we are.

Welcome to the Thoughts of Taylor.

——————
I want to talk about integrals. I’m pretty sure a lot of you nerds who read these blogs know what an integral is, but my mom, who also reads these blogs, does not. So for Mom V. (<3), here’s a crash course.

First you have an arbitrary function. Let’s say you’re plotting the velocity of something as it moves for a set amount of time. You went for a run, and you were wearing a fancy Fitbit, so you were able to keep track of your speed at any given time during the run. If you plotted every single one of those points, it would form a curve like this:

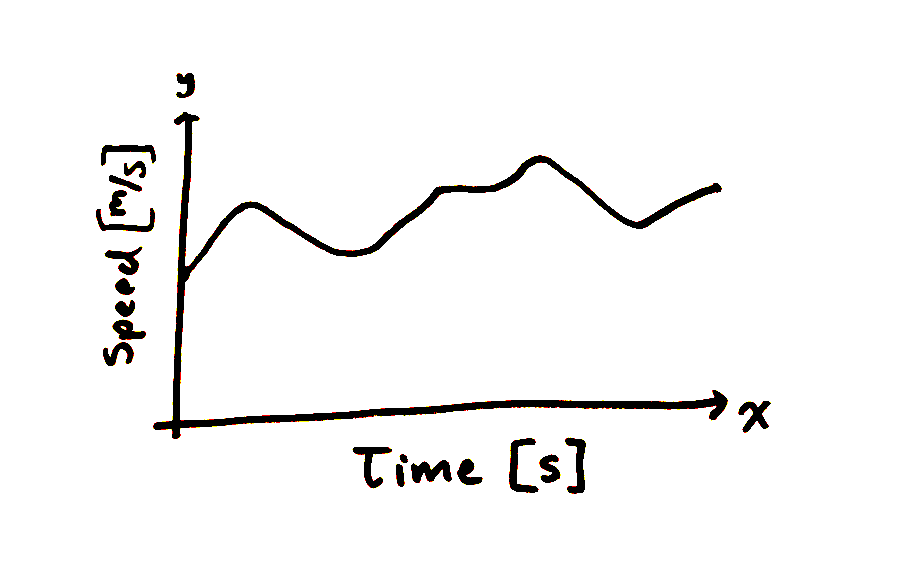
(Note the civilized metric units)

But let’s say that you didn’t care about how fast you were going at any given time. You just wanted to know how far you had run (pretend the fancy Fitbit only tracks speed, not distance). Taking the integral of your speed-time graph will do just that. An integral is just a fancy way of saying, “find the area underneath the curve”:

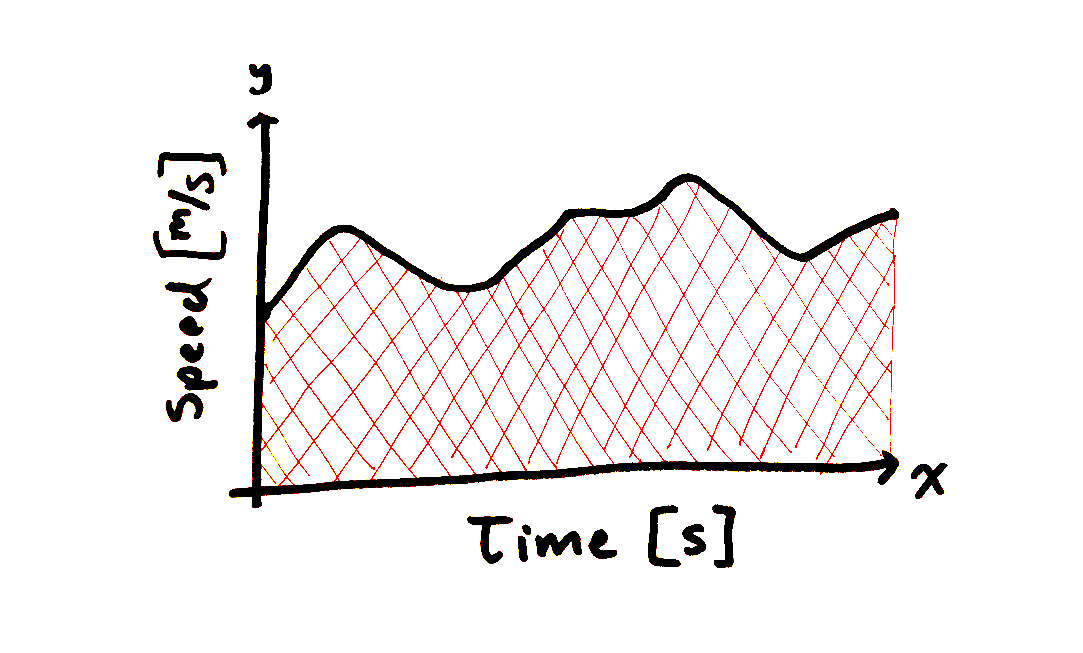
But area is length times height, right? Here the length is straight, but the height is all curvy.

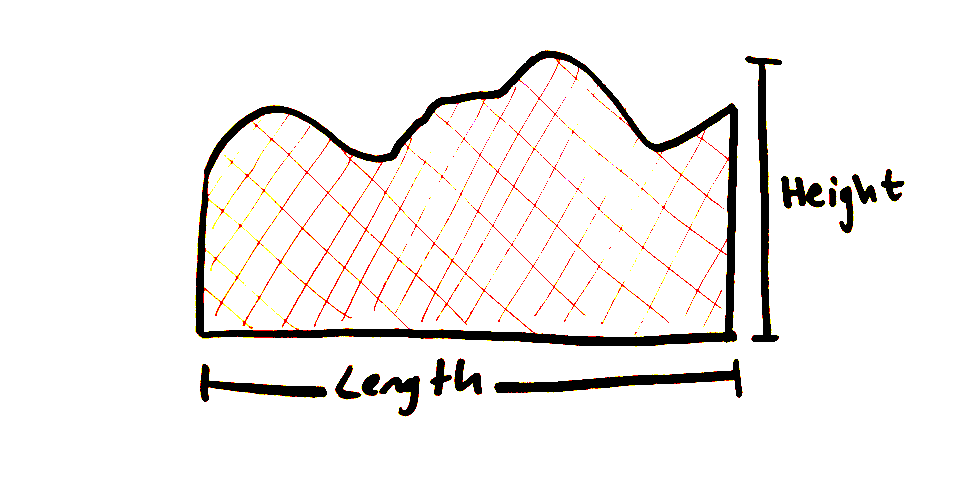
Now what?

This is the beauty of an integral. You take the large, oddly-shaped area under the curve and zoom in:

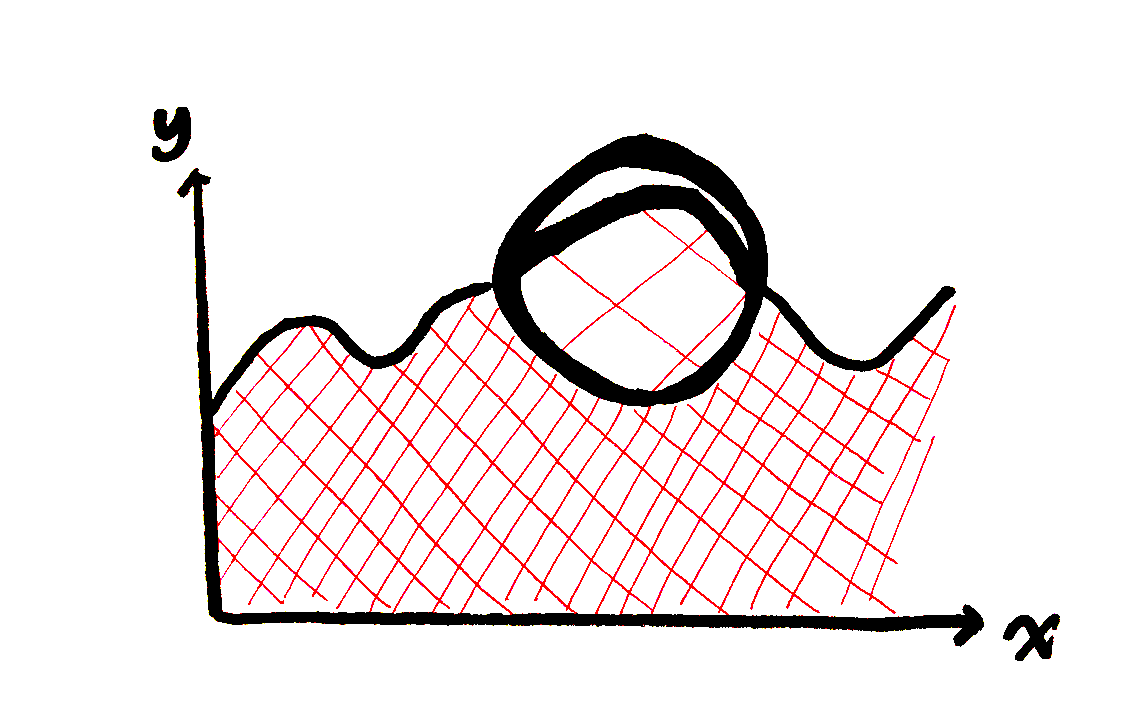
And then keep zooming in:

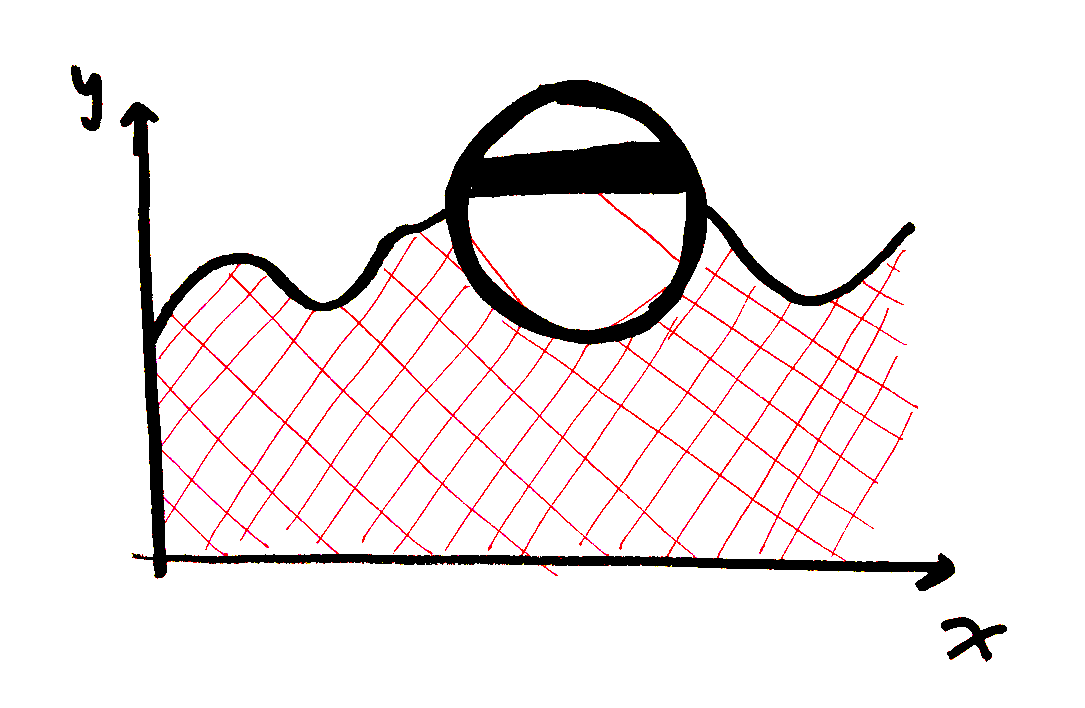
And then suddenly, if you zoom in far enough, the curve isn’t a curve anymore, it’s a line. And you know what to do with lines, you multiply the length times height. So you can calculate the area of that little rectangle. And then you move a little farther in the x direction, and you add that little rectangle, too. And then you keep going, and keep adding little rectangles, and suddenly the large, complicated problem is just a simple sum of a lot of little rectangles. Your run is no longer a start and an end, but a million little slices of area in between:

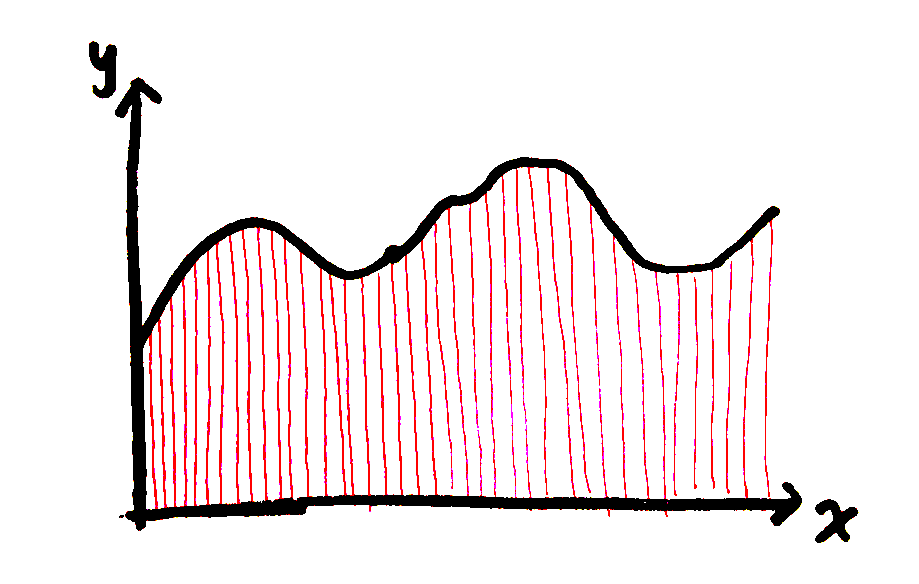
Cool. Now we all know integrals. So what?

I don’t want to be super dramatic and say something like, “Life is an integral”, but like, life is an integral. Or maybe it’s just MIT that’s an integral, and once I graduate I’ll discover that life is actually a derivative or something (@Mom V. a derivative is the opposite of an integral, so this is a joke because then it would be like my time at MIT prepared me for the wrong thing and then when I get thrown out into the cold, cold world graduate I’ll be completely lost and confused. Ha. Ha.)

One part I didn’t mention was the y-intercept. This is where the function crosses the vertical axis. This intercept is also the height of our first little rectangle. In the running example, this would be your starting speed. If you believe me for a second and pretend that my time at MIT can be plotted in Cartesian coordinates, that first little rectangle represents the baseline education I had when I started college.

I arrived on campus with a relatively small first rectangle, but I didn’t know it until I saw everyone else’s at Orientation. Some people came to MIT with an incredibly high y-intercept. Their first little rectangle wasn’t little at all. It was a huge rectangle, filled in with AP classes and Math Olympiads and coding experience and perfect SAT scores.

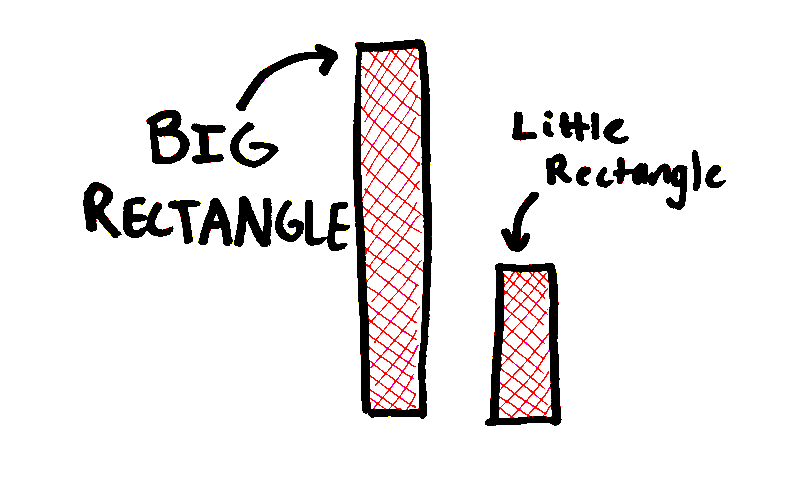
Every time I looked at mine, it seemed to shrink a bit more. Especially once classes started and all I could see was a lot of Big Rectangles in the front row of the lecture hall, answering the professors questions when I barely could follow along, and acing tests that I struggled to even finish on time. It was clear that my self- taught calculus and 9th grade biology knowledge was not going to cut it anymore. I set about trying to hide my Little Rectangle.

What if they find out you don’t belong here?

—————————-

Sometimes I feel dumb; other times I am just completely, objectively dumb. One highlight/lowlight was staying up until 7 AM to finish a pset 7 days early, because I forgot to check the date written at the top of the page and thought it was due the next day:

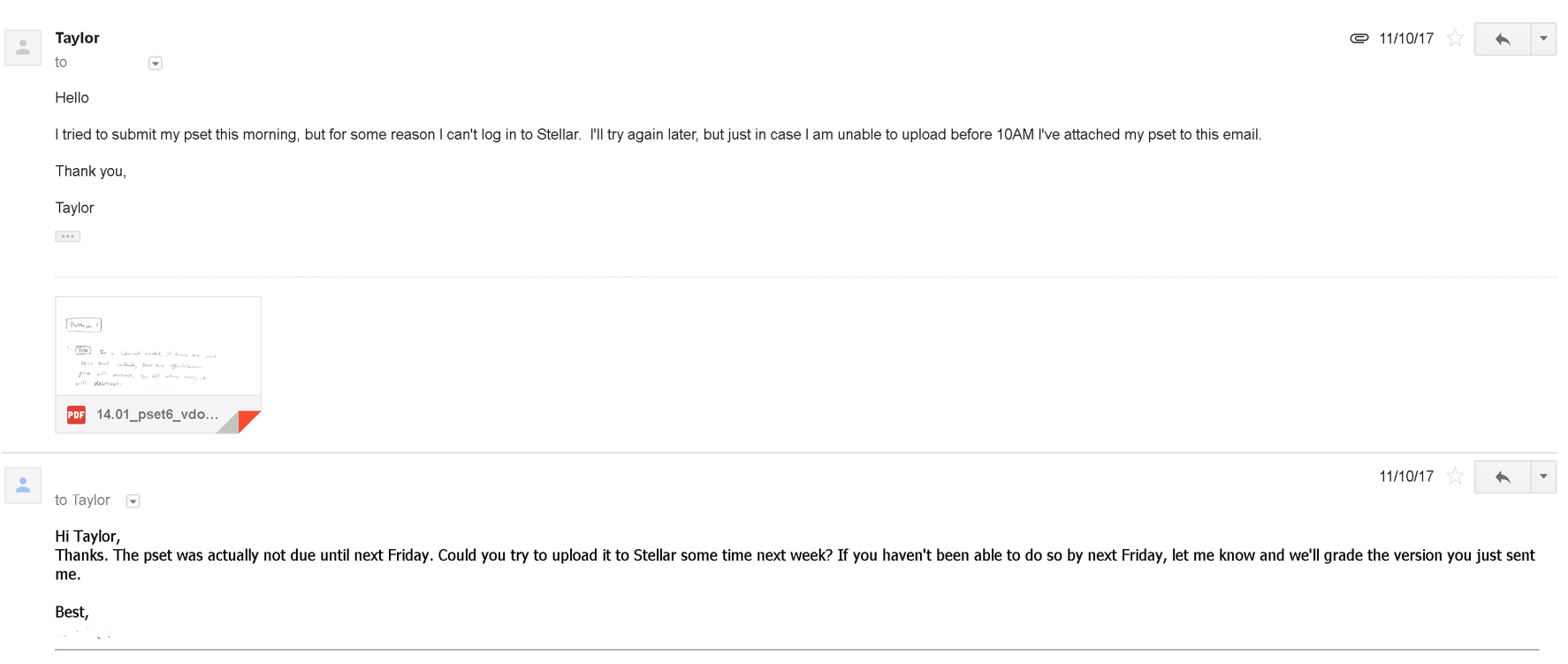
After some sleep, I had a good laugh. Eventually though, it hit me how sad the whole situation was. The pset took me all night to complete because I got caught up by a couple concepts that we hadn’t covered in class yet, and would be discussing in next lecture. It had never even crossed my mind that the reason I felt like I’d never seen the material before was because I had, in fact, never seen the material before. Instead, I berated myself for not paying close enough attention, for not understanding, for being too slow.

Why can’t you get this?

I wish I could say this was the first time I did the wrong pset, but that would be a lie. I really need to check the due dates on those things.

I also really need to stop equating understanding with intelligence.

—————————-

That’s what has been hardest for me to remember. That not understanding something doesn’t mean I’m not learning anything at all. It doesn’t mean I’m not intelligent, it doesn’t mean I’m going to fail. It just means that I need to find a way to understand.

Freshman Taylor did not get this at all. Sure, I learned a lot. I learned so much that some days I actually didn’t know if I could cram any more into my brain. Everyday I was adding a little more to my row of rectangles. However, I still wasn’t judging my progress on a day-to-day basis. I was looking at the Big Rectangles. I was looking at my Little Rectangle. I was looking far, far down the x-axis to where I wanted to end up and forgetting that I wasn’t going to get there in one step. I felt so far behind and I was mad at myself for not learning fast enough; for struggling so much when it felt like I shouldn’t.

Why can’t you figure this out on your own?

—————————-

That’s the story of the GIRs. I convinced myself it would be okay once I started my major. I did a UROP over the summer and fell in love with mechanical engineering. I thought that this would make it easier. I thought maybe Sophomore year would be better.

If freshman year was a firehose, sophomore fall became a flash flood. Failed tests and dropped psets and confusing lectures kept raining down on my head as I desperately tried to stay afloat. I got that email a couple of days after the second exam. I had dropped two psets and a class just to put every waking moment into this class. I took to walking around campus with an open notebook so I could squeeze in a few more statics equations between lectures. I would sit alone, late into the night, spending hours and hours on a single question, only to eventually turn in the problem set incomplete. Basketball practice became an inconvenience that made me late to office hours on Thursdays. It got to the point where I would literally dream of stress and strain problems, and wake up panicking in the middle of the night because I had messed up a free-body diagram. Apparently none of that mattered, because I was still failing.

Why is this so difficult for you?

Everyone else understands….

…maybe you just aren’t smart enough.

—————————-
And now back to the rectangles. Throughout all of my struggles the first two years, I never realized that the problem wasn’t my Little Rectangle. I probably wasn’t ever even that far behind, but I had convinced myself that I was, so I tried to hide it. I would spend hours on a problem before I asked for help. Even if I was completely lost in recitation, I would never raise my hand and ask the TA for clarification. I was determined to do everything myself, because up until this point in my life, I had never encountered a problem that I couldn’t solve by outworking it. I was focused on the big picture, this vague notion of “being smart”, and not on the only aspect of my academic life I could actually control- the production of those incremental rectangles.

—————————-
Freshman year was a struggle in more ways than just academic. For the first time in my life, even basketball was hard. There was an entirely new system of offense and defense to learn, and many days it just wouldn’t click for me. I had to think so much on the court I could barely move. I was frozen in place, my mind racing to remember the steps to the complicated dance of screens and cuts and post-ups, all of which had to be coordinated with four other people simultaneously. I couldn’t do anything right. The sport I loved had turned into yet another impossible pset, and I was behind again.

Wow, something else you can’t do. Shocking.

Basketball is probably what grounded me in the long run, though. Much like life and MIT, basketball is, (say it with me), an integral. And even if I didn’t realize this academically, it started to make sense in my athletic life. On the basketball team we call this day-by-day process of making rectangles “controlling the controllables”. Instead of focusing on some far-off, lofty goal of a championship, every day you go to practice. And every practice you ask yourself, “What can I do today to get just a little better today than I was yesterday?”. Maybe today I want to make sure I box out every single time a shot goes up. Maybe today I want to execute my spot in all of the plays perfectly. Even that can be broken down further- I’m going to cut hard on this play. I’ll focus on this drill, on this possession. In this moment, I’m going to get a little better. And eventually all of those days, all of those little moments, every single box out and cut and screen, all (hopefully) add up to your end goal of a championship.

This made so much sense to me in the setting of Rockwell Cage. However, it’s a bit harder to track progress this clearly in academics. How can you really tell if you’re better at thermodynamics today than you were yesterday?

To be completely honest, I don’t know. Theoretically you should be able to judge your academic progress by tests, but that seems like the easy way out. That’s like jumping from the start of the season to the championship, and forgetting every practice in between. That’s like looking back judging yourself based on your Little Rectangle, and ignoring all of the other rectangles you’ve made since. When you bomb an exam, maybe that’s when it’s time to think about the integral and not the rectangles for a minute. It’s reassuring to be able to step back and look at the sum of the parts sometimes. Because even if you fail the test or lose the championship, all of those rectangles still add up to something.

—————————-

And now we’re going to wrap up the whole Big/Little Rectangle saga. (Stage fright is only part of the reason why the Thoughts of Taylor rarely makes an appearance; meandering is a big factor). As a junior, I’m so far along the x-axis of MIT I don’t even notice my Little Rectangle anymore. The problem now is I forget that I have any rectangles at all.

I know I still need to work on this. There are only so many hours in the day, and if you spend half of them struggling on a pset for a single class because you’re convinced you should just be able to get it, and you have three other classes, and you’re trying to play sports/look for internships/have friends/eat and sleep sometimes… this is unsustainable and I have learned that the hard way.

I know I still need to work on this. I’m still self-conscious when it takes me longer to understand something than it does for my classmates. I still compare my progress to others. I need to ask more questions. l need to remind myself that being confused by a lecture or struggling with a problem doesn’t define me. Even if I don’t have a rectangle to show for the day, I still have all of those other rectangles behind me, proving that I’ve understood a lot of lectures and I’ve finished a lot of problems.

I know all of this is true, or at least somewhat true, but I’m still not convinced. I’ve spent the last three years telling myself to just keep going, just keep working harder, and it will get better. It sounded desperate for a while, and now it’s just a whisper it will get better it will get better it will get better itwillgetbetteritwillgetbetter. After a certain point it just sounds hollow. But in the meantime, maybe throwing my insecurities into the depths of the Internet is a step in the right direction:

“Hey everyone, look at my Little Rectangle! There are a lot of things I don’t know. I’ve failed tests and dropped classes. Sometimes IHTFP. Sometimes I really HTFP.”

That felt good.