
Math = Broken by Snively '11
Whatchu know about math?
This OFFICIAL MIT blog is probably not designed for late-night delirious whims of posting. Oh well.
So, it’s late (3:00 AM) and I just finished most of a Diff Eq. PSET (I started at 10:45 PM, it’s been a long day).
Here’s when you know it’s time to go to bed.
Roommate Jon: “Did you get Part II, 4) d?”
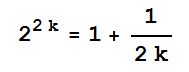
Me: “No, solving for k was impossible, not even Mathematica could do it.”
Jon: “I know, the same thing happened to me. I think I figured out how to do it though.”
Me: “How?”
Jon: “Here, look what I did. . . ”
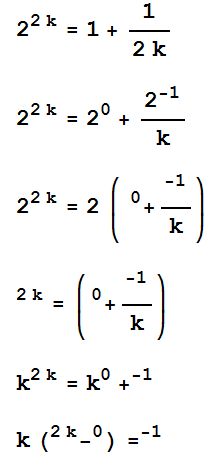
Me: “. . . what!?!”
Jon: “Wait, you can’t even solve this! I hate math.”
Me: “I’m going to bed.”
What makes solving that equation for k fall under the category of “differential equations”?
Please don’t post the answer so soon. Let many solve it…then please post it.
Take care Snively.. No more late night Math for you Lol!
Lol!
-.8563 works
This seems like as good a time as any to post my mathe…lingual proof that MIT is better than Caltech:
MIT ~ Brains.
Caltech ~ Brains.
MIT = Massachusetts Institute of Technology.
Caltech = California Institute of Technology.
MIT-> Good with science/technology.
Caltech-> Good with science/technology.
Germany-> Good with science/technology.
German-> Language of Germany (good with science/technology).
mit = German word for ‘with.’
cit = not the German word for ‘with.’
Caltech = not the German word for ‘with.’
MIT -> “German word for ‘with'” Brains.
Caltech -> “Not the German word for ‘with'” Brains -> Not with Brains -> Without Brains.
q.e.d.
Questions? Comments? Can I help clarify? :D
How long is the PSET?
Just looking at it k = 1/2
hmm, jon and michelle came by btb and did this problem with me around midnight last night. i thought i solved it.. haha maybe not. turning it in anyways.
and in response to alexander — the comic is from caltech’s prank on The Tech from last year’s cpw; it was supposed to be a parody of xkcd.
Thanks Sara! Jon mentioned that you had worked on it, and that you made numbers up, and kinda just smashed stuff together until something worked. Whatever does the trick.
And yes, although it looks like an XKCD comic (it was indeed parodied), Sara was right. It was the comic CalTech hacked my CPW with. I like to have fun with it. In fact, it’s a greeting now between me and some friends.
“Math.”
“Math.”
“LOL.”
In answer to some of the other questions (mainly as to why this looks nothing like a differential equation), that’s because there was a whole lot of work done until this point and this is the boiled down version of an initial value problem. Do you want to know what the whole problem is?
Part II #4
Thanks for all of the help, now I may actually get this right when I turn it in this afternoon.
Alright, will the question only include the first order nuclear reaction formula like T(1/2)= 0.693/k and another one from which it is derived?
I am asking this because I might be missing some important theory taught at the classes of MIT( Sigh….How I wish to be there).
Is the subtitle a reference to the YouTube video by TI-84?
If only math worked like Jon thinks it does at 3:00 am, it would make my life much easier…
@Suzanne
Click the link in the subtitle. . .
Ugh. I don’t see what the problem is.
If you just want the real values of k, you can plot both sides and see where they intersect:
k = .5
k = -.76
Of course, if you replaced the k on the right with a T, and wanted K(T), I can’t see how you’d do that.
I’m not that good with math, so there’s probably just something I’m not seeing.
@Libin
The question only uses T(1/2) = Ln(2)/k
The trick is to figure out dx/dt and then solve for x. Use your known value of x to set up dy/dt and solve for y, and then use everything you know so far to set up dz/dt solve for z.
Hint: For part 4, when Kr is at a maximum, that’s an initial value problem with t=2ln(2) and dy/dt = 0.
Oh, and this may help in general:
http://scitation.aip.org/journals/doc/AJPIAS-ft/vol_71/iss_7/684_1.html
yeah, the first three parts are fine enough.
In d) How comes you equated and got the result that you have blogged. Throw some light man on it man.
I might be missing something but…isn’t the function on the left strictly increasing, and the one on the right strictly decreasing, so the given equation has at most 1 solution? Then 1/2 would be the only solution.
Awesome post, loved the YouTube video!
I’m not sure. I didn’t actually get an answer that boiled down to that. While my answer didn’t work either, this is the answer that some other people got. It was just an un-fun problem.
It’s cool, buddy. Having 2 indeed 3 nuclear fissions all together..never got to solve something like this. How did you link up z(t) with y(t) and x(t). Sorry for this repeated postings..I am really sorry. LOL.
I got
k=0.5 or k=-0.765
沙发!
(that’s Chinese…probably not the best place for this heh~)
(meaning first in forums)
the comic’s from the Tech right?
GETTING THE ANSWER IS NOT THE POINT BUT THE WAY IT IS SOLVED…A GRAPHIC CALCULATOR CAN GET THE ANSWER BUT ONLY WE CAN SOLVE IT.
You have been having a long day. Did you see the one with the square root sign? I (heart) math jokes!!!
Sorry for the double post but actually the comics from XKCD (I think).
I tried taking log and solving on both sides and then substituted 2k=u and and and and and and and…………….why can’t i do it???
Yea…..now i’m going to sleep to….!
PLEASE POST THE SOLUTION TOO!
Hey! Please don’t do this to math!
Oh…btw…i loooooooooooooooove your bbbbbbbbbbblllllllllllllloooooooooooooooooooogggggggggggggggssssssssssssssssssssssss!!!!!!!!
k=0.5 by…well, guessing.
it’s 4:30 PM in my timezone, so apparently my brain’s working alright
Oh jinziling, the points of intersection will be the solutions, and there are TWO! k=-0.75(approx) I just posted the graph on myspace…
alright all you nooby mathematicians,
k= .5
k= 0
DID ANY OF YOU BOTHER TO CHECK YOUR OWN ANSWERS!!!
2^(2(.5)) = 1 + 1/(2(.5))
2^(1)=2 and 1 + 1/1 =2
2 = 2
2^(2(.5)) = 1 + 1/(2(0))
2^0=1 and 1 + 0 = 1
1 = 1
nothing else works
edit*
for the bottom one
2^(2(.5)) = 1 + 1/(2(0))
2^0=1 and 1 + 0 = 1
1 = 1
this is supposed to be
2^(2(0)) = 1 + 1/(2(0))
2^0=1 and 1 + 0 = 1
1 = 1
You, um, just divided by zero.
forgot to log in again, above is mine as well
oh sorry i’m only in 4th grade
didn’t know you can’t divide by zero =0
Mathematica CAN do it…use FindRoot.
it’s 4:30 in morning and i’m still awake
I think I first knew that math was broken when I read about the Dirac delta “function.” (It’s actually a distribution…but don’t tell the physicists that!)
*coughs at MIT math wiz*.
I’m actually kind of happy that I managed to solve that The PSET was too much to read on a snow day though.
The PSET was too much to read on a snow day though.
Did you try putting LOG on both sides then simplyifing it then solving for K?
Nice blog btw.
This is how to solve it:
let 2^(2k) = a
therefore 2k = ln(a)/ln(2)
then substitute into the original equation…and manipulate it untill you get
a^a = 2a
(btw at one point you are going to have to take e^ of both sides…..post it snively!!)
The answer you get is a=2….then substitute back into 2^(2k) = a and find k….it turns out to be 0.5!
^^ (“post it snively” as in post the solution i emaild you!)
1. I love that video! Whatchu know about math, whatchu know about math, etc. :D
2. Hahaha your response to the nonsensical method is probably the funniest part of the whole thing.
“…what?!”
OH and did you know? “?!” has its own name! I heard it was called an interrobang.
I think what Kaled did was an elaborate way of finding one of the roots by inspection. In fact, as jinziling showed, k=1/2 could be deduced from the original equation.
However, I think finding the second root (k=-0.765), a numerical approach would have to be taken. A good method would be graphing the rhs and lhs and finding the intersection points, as Tanmay did.
I SOLVED IT….MIT ACCEPT MEEEE!!
(I emailed you the solution snively, post it if you want to!)
i’m sure snively can do it too…he’s just tired
oh and btw, i love your blog snively!!
and im sure he can to do it too…..its just a simple substiution!!
It’s diff Eq PSET and the question has just one variable??Hilarious!
Snively has posted it under health and safety.. Much more Hilarious!
Oh Oh Oh!
Set it to zero and use Newton’s Method!
My Calc teacher would be so proud.
Negative values of k won’t be possible; it’s decay constant after all…So .5 is the only solution.
The part’s over every1…move on….next blog, next blog!!!
18.03 Problem Set 1
“Part II contains more challenging and novel problems. They will be graded with care
(Complain if they are not!) and contribute the bulk of the Homework grade.”
LOL!
That 18.03 pset was a beast. It was the reason why I stayed up until 5:15 AM last night (and I guess I started much too late…=/). I was so delirious at the end.
The calculations for #4 was a beast. All that work to get “ln 2” at the end. How anticlimatic.
^ Oops, I don’t know whether I should say that, but I guess everyone turned it in already…
Hmm I got 0.5 without any fancy manipulations or substitutions. Maybe I used Jon’s kind of math a while ago…
lol, that’s because your roommate did 2^{2k} = 2*{stuff} –> 2k = stuff
hahaha, I love Jon’s method. He does what he wants and doesn’t let the rules of math hold him back. =P
@ Oasis
I disagree, when an answer comes out to something simple like that, I think back to my calc teacher’s words of wisdom,
“It’s too beautiful to be wrong.”
Actually, that problem was designed so the answers would be pretty, and said as much in the text of the problem. Very considerate of our professor, don’t you think?
It was still a pain in the butt though. :D
So, uh, Snively….I guess you have to cite all of the bazillion people that posted on this blog entry as your sources of help, eh?
Lol…Funny Eric.
So have come to a suitable solution( method indeed) yet?
Impressive… however why use all those fancy equations… I believe that what Snively and the other people did were okay… however Newton’s Method???? heh this one was an interesting question took me about… well 15 -20 mins to solve. My calc teacher was proud…
Strangely enough, I actually have a serious question about life at MIT. Most Excellent Snively, is 3:00 AM a normal bedtime for you? How late do your PSETs usually keep you up? I’m fairly sure that I’ll be majoring in some sort of engineering (right now I’m leaning towards Course 10), and that’s no picnic anywhere. So how bad is it at MIT? What are the consequences of getting so little sleep?
That 18.03 pset was crazyyyy……ahhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
just get a=1/2 by solving get the other soln. as I get when done by graph.
that is pretty funny stuff – that Caltech spent the time to hack MIT’s magazine and call them nerds. I got to admit, though, that is a joke with style.
I conjecture that the more random/sillier a blog post is, the more comments it gets.
Or maybe it’s just the math.
It’s almost in a form that you could attack with the Lambert W-Function.
This post absolutely made my night
That was a wonderfull post!
Could you please tell me the tentative dates by which the RA’s can hear from the MIT admissions office?
Thank you!
I can make a really logical guess but Admissions will announce officially soon.
I’d place decisions at 11:48 AM EST on March 22nd
@Libin
Here’s my logic:
Decisions always come out mid-march. They’re also always released online on a Saturday afternoon (at least in my experience). That narrows it down to the 15th or the 22nd. Two years ago they released on Pi Day (March 14th). Last year they tried to release that early but couldn’t pull it off because of the larger number of applicants. They have even more applicants this year, so March 15th looks unreasonable. March 22nd looks pretty reasonable though.
As for the 11:48 AM, decisions are officially released online at 12:00 PM EST, but they actually sneak them on about 12 minutes prior. Haven’t figured out why yet, but it’s a handy little bit of info.
Sooooo, that’s my thinking. This could be completely wrong so don’t quote me on it (although I’m an admissions blogger I don’t actually know the inner workings and secret stuff from the admissions office), but it’d be safe to guesstimate.
Find:
Sum from k = 1 to infinity of k / (5 ^ k)
Hey Snively, what is the logic behind the date you mentioned?
Woah woah woah,
Don’t be hatin’ on Newton’s Method.
It’s Legitimate.
Just say that 0= 2^2k-1-1/(2k)
So then F(k)= 2^2k-1-1/(2k).
And then K2= k1 – F(k1)/F'(k1)
So just pick any old number for k1 to find k2.
And then, K3= k2 – F(k2)/F'(k2)
So just do that infinity times and you get the right answer.
It sooooo simple why would you just want to use that complicated algebra and substitution mumbo jumbo.
Newton is where it’s at.
thx Khaled Saad.
that really helped a lot… solved it
I know there must be some way other than compute it numerically… especially when there is a rational number…