We Stan Matt Parker by Paige B. '24

In my junior year of high school, I started taking single-variable calculus at my local community college. I began to feel like a real college student (at least, for a high school student). But I remember sitting in lecture, and at some point thinking: “is this what mathematicians do all day?”, which was a question quickly followed up by: “wait,,,, what do mathematicians actually… do?”

And it’s not like I haven’t had this question before. For example, I asked these questions when I was learning about how to multiply multiple-digit-numbers in elementary school, thinking to myself “surely mathematicians don’t sit in their offices all day multiplying bigger and bigger numbers”. But when I was younger, I knew that this couldn’t be the case. I just had no sense of what college-level maths looked like. So I ate my mathematical-vegetables and went on with my life.

So ending up in my first ever college class and asking the same questions was frankly a bit of a shock. And don’t get me wrong, calculus is beautiful, and (some) mathematicians do use calculus in their day-to-day life (including myself!). But calculus felt too… closed? I guess? I’m sorry, I am missing the exact right words for this, but to put it frankly: Calculus felt like, finished in some sense. It felt too polished. Like, what mathematician with a PhD is sitting in their office “researching” how to solve the integral

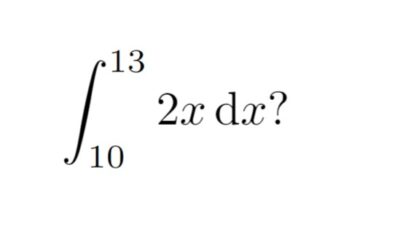
The answer is 69.

So anyways, I’m taking this calculus class and trying to figure out a) what maths after calculus looks like, and b) if I want to actually do that math. Then, I found a maths comedy special by Matt Parker.

Matt Parker has done a lot but you may have most commonly seen him on NumberPhile, or you may have read one of his books Humble Pi or Things to Make and Do in the Fourth Dimension (to name a few). You may also know him from the Parker Square.⁠01 listen I said I'd try not to mention it, not that I'd try that hard.

In this comedy special, Matt Parker talks about the concept of 4-dimensional space. I’ve written about 4-dimensional worms before (here and here), but let me discuss the concept here again too for those who may be unfamiliar (as I once was before I watched Parker’s comedy special).

You may have heard that we live in a three-dimensional world, but what does this mean? Well, one way we can describe this is that we can move in three directions: up/down, left/right, and forward/back. Alternatively, you can look at the corner of the room you are in, and see how many walls it takes to form the corner (i.e., three). The same concept is true in lower dimensions. For example, to picture two dimensions, simply imagine a piece of paper with a square on it. Notice how it takes two lines to “form a corner” of the square. Similarly, characters in 2-dimensional video games really only need two directions to describe where they are in space: up/down and left/right. You can picture an old-school 8-bit Mario moving left/right, or up/down, but there are no other directions for the 8-bit mario to move in (at least, not until Super Mario 64). Lastly, we can think of lines being one-dimensional (like the number line).

But what about four dimensions? We can’t quite necessarily picture 4-dimensional space well, but sometimes people refer to time as the fourth dimension. If we consider time to be the fourth dimension, then our four directions would be:

Up/Down, Left/Right, Forward/Back, and Future/Past.

Side note: viewing time as the fourth dimension is actually what my worm blogposts are about. In any case, when mathematicians talk about four dimensions, they typically mean something slightly more abstract and slightly more physical (in a way I will explain right now).

One way we can make dimensions more “physical” is to think about how we measure “volume” in those spaces. For example,

• 1D: Length: We can measure the length of a line segment.
• 2D: Area: We can measure the area of a rectangle via the formula base times height, where both the base and height are in some sense 1-dimensional (they are just the lengths of the sides of the rectangle).
• 3D: Volume: We can measure the volume of a rectangular-box via the formula base times height times width (notice that this requires knowing three 1-dimensional parameters…)
• 4D: ?????? It’s kinda unclear! But, if we wanted to find the volume of a four-dimensional box, it would make sense if it required four 1-dimensional parameters, like base, height, width, and then some other length in a different (fourth) direction.

Hopefully I’ve done a good enough job of trying to give a sense of what four (or more) dimensions kinda means.

In any case: Matt Parker. In Parker’s comedy special, he spends like an hour trying to explain how we can try to visualize the fourth dimension. And, sure, we can define the fourth dimension abstractly and mathematically, but actually trying to visualize higher dimensions is a bit of a difficult task! I think Matt Parker does a really good job of this, and highly recommend watching the video.

Upon watching this special, I started to realize that I really wanted to understand four dimensions better. I wanted to understand five dimensions; six; seven; hell, why not n-dimensions??? (by which I mean arbtirarily-many dimensions).

But I was only in single-variable calculus, and I didn’t really understand do mathematics in 4 dimensions, let alone n. So I forgot about it and moved on with my life.

Cut to my senior fall of high school when I’m taking multi-variable calculus and linear algebra, and OHMYGOD I AM FINALLY DOING MATHS IN HIGHER DIMENSIONS. Granted, most of the maths is in three dimensions, but doing calculus in three dimensions makes it clear how one would do it in higher dimensions.

But it was still unclear to me how I could picture five+ dimensions. I mean, because of Matt Parker’s comedy special I could somewhat visualize four dimensions in my head, but five+ dimensions seemed just out of reach. And surely, there wasn’t some way to use mathematics to picture higher dimensions.

All the while, I find myself applying to colleges for undergrad. For one of the application essays,⁠02 note that I applied through QuestBridge and this was a QuestBridge essay question I found myself writing about a “topic you have explored simply because it sparked your intellectual curiosity”. In particular, I wrote about being inspired by Matt Parker and wanting to learn how to picture n-dimensions in college. But surely that wouldn’t happen.

Cut to being at MIT and doing maths research and OHMYGOD I CAN USE MATHEMATICS TO PICTURE n-DIMENSIONS. Most of my research at MIT for the past three years has been about trying to visualize n dimensions (in some sense). I love this research. I love that I can roughly explain my research to other people, and I love that I do this work in arbitrary dimension. In fact, most of why I like this type of research (in the field of maths known as analysis) is because I like being able to explain what it is I study to other people. And hell, this is part of the reason I fell in love with the concept of mathematics in the first place: Matt Parker’s ability to explain the concept of four dimensions to people in a comedy special is exceptional, and I wanted to one day be able to do this one day. But surely, I wouldn’t get the opportunity to explain what I research to other mathematicians until I was a professor.

Cut to being a senior at MIT, and BEING INVITED TO PRESENT ON MY MATHEMATICS RESEARCH AT THE JOINT MATHEMATICS MEETING (JMM). For those who don’t know (and to be completely fair, I didn’t know what the JMM was until last year when there was one in Boston), the JMM is the largest mathematics conference in the world, and I was invited to present at two of the smaller sessions in my area of analysis! It was my very first JMM presenting material, and I presented on all the n-dimensional research I and others in my field have been working on. It was so much fun, and I got to meet a lot of really cool people.

One of those cool people I got to meet was MATT PARKER!!

It’s Matt Parker!! and me!! in a photo!! together!! not photoshopped!!

During the JMM, there was a Mathematics Art Revue show with jugglers, dancers, poets, ⁠03 Harry Baker is my favorite poet, give this poem a listen and then go listen to <em>Paper People</em> and more, and the show was being emceed by Matt Parker. After the show, he was in the lobby meeting people and signing people’s names in binary (he signed my JMM nametag!).

I told him about how much his comedy special influenced me. I told him how I wrote about it in my MIT application, how I was inspired to continue investigating mathematics, and how it led me to pursue mathematics research that I was presenting on at that year’s JMM. All because of a maths comedy show that I watched ~five years earlier. How the time flies.

P.S.: If you’re interested in learning more about my research and what mathematics research looks like, my plan is to write about this in my next blogpost! Stay tuned :)

P.P.S: I used “maths” instead of “math” throughout this blogpost, and fun fact: when I applied to undergrad, I did used “maths” or “mathematics” instead of “math” in all of my essays.