
Lessons from Loomis and Whitney by Paige B. '24
a math month post
Unfortunately I don’t think I will be talking about the duality between points and lines that Andi alluded to in his post on duality (though maybe I will later this month/semester we will see). But this is a post for MITAdmissions Math Month, and thusly there will be some math. And perhaps some thoughts about life at MIT too. If you’re not as interested in the math stuff, you can scroll on through to Part 2 where I talk about some thoughts about life at MIT :). The math in the first part is some material I learned (and still love) from the UROP I did the summer after my first year at MIT.
Part 1: The Loomis-Whitney inequality (aka the math part)
Take your favorite set of finitely many points out in the plane, i.e. in $\mathbb{R}^2$. Let’s call this set $A$. Now, suppose we look at the “shadow” of $A$ on the $x$-axis and the $y$-axis, and let’s call these sets $\pi_x(A)$ and $\pi_y(A)$ respectively. If it helps you to see it written down mathematically, we have the functions $\pi_x(x,y) = x$ and $\pi_y(x,y) = y$. See the below diagram for further clarity.
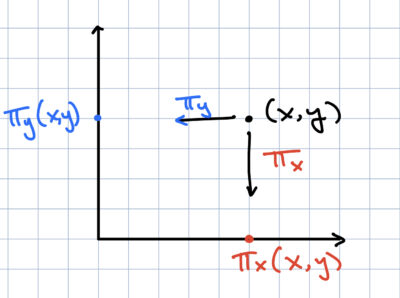
Projections of the point (x,y).
One question we can ask is the following: If we only know about the size (i.e. how many) points there are in the shadows of $A$, can we get a good bound on $A$ itself? The answer, in 2-dimensions, is quite immediate: Yes. For every point in $\pi_x(A)$, we can draw the corresponding line that maps to this point under the projection, called the fibers of this projection. Similarly, we can draw every fiber corresponding to $\pi_y(A)$, and we will notice that the set $A$ must lie at the intersection of the fibers from the $x$-axis and the fibers from the $y$-axis (depicted below).
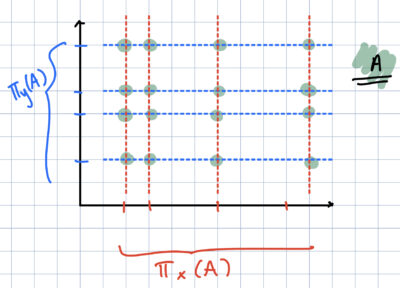
The set A here (in green) is contained in the fibers of its projections onto the x and y axes.
To write this down mathematically, what we have proven is that \[A \subset [\pi_x^{-1}(\pi_x(A)) \cap \pi_y^{-1}(\pi_y(A))],\] and as such, we have that \[|A| \leq |\pi_x(A)| \cdot |\pi_y(A)|.\] Or, if you prefer more directly, we have \[A \subset \pi_x(A) \times \pi_y(A),\] (though this won’t generalize in higher dimensions– at least not what I am going to present in higher dimensions). I.e., the number of points in $A$ is bounded by the number of points in the projection onto the $x$-axis times the number of points in the projection onto the $y$-axis.
Okay, but how good is this bound? To understand how good this bound is, we can first consider dimensional analysis— a technique that is taught early on in 8.01 (Classical Mechanics) at MIT. The idea is the following: Suppose that we measured “volume” in $\mathbb{R}^2$ in square inches, i.e. $(\text{inches})^2$. If this were the case, then the shadows of $A$ onto the $x$-axis and the $y$-axis must be measured in inches. Therefore, looking at the above inequality (and replacing $A$ with its units and $\pi_x(A)$/$\pi_y(A)$ it their units), we get that \[(\text{inches}^2) \leq (\text{inches})\cdot (\text{inches}).\]
Given that we have inches squared on both sides, we might suspect that our inequality here is very good (for arbitrary finite sets in $\mathbb{R}^2$), and in fact it is! To see just how good out bound is, all we need is one example of a set $A$ where the inequality is an equality, and here is that example:
Take your set $A$ to be the set of integer lattice points, where each coordinate is an integer between $1$ and $N$ ($N$ here being some large number). Then, in total, we have that $|A| = N^2$ while $|\pi_x(A)| = |\pi_y(A)| = N$.
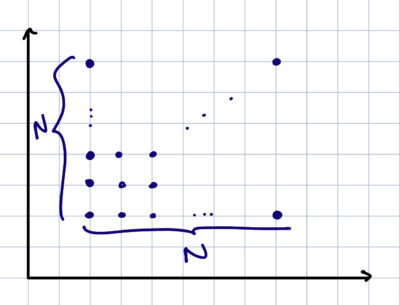
A good example to keep in mind that shows that the inequality we proved is in fact (sometimes) an equality). Can you find another such set that leads to an equality?
Hence, we have found a set where the inquality is an equality, and thus out bound is as good as one could’ve hoped for.
Exercise: Find an example of a set with roughly (up to some constant) $N$ points, whose projection onto the $x$- and $y$-axes has precisely $N$ points each. I.e., find an example of a set where the bound we got is really really bad.
Okay cool– that was a lot of math (and it is about to be quite a bit more in just a second), but let’s take a breath. What did we do? Well, essentially, we bounded the area of a set by the lengths of its shadows. And though this proof was fairly short, we might expect that the same thing holds in higher dimensions, which is in fact the case. In this post, the most we will do is study this in 3-dimensions, which we do now. The proof will be a little bit lengthy, but that is kinda the point of this blogpost (see Part 2).
Let $A$ be a finite set in $\mathbb{R}^3$, i.e. a bunch of points out in 3-dimensional space. Our goal is to (again) bound the number of points in $A$, i.e. $|A|$, by the number of points in its projections (i.e. projections onto the $xy$-, $yz$-, and $xz$-planes). Note: we denote these projections: $\pi_{xy}, \pi_{yz}$, and $\pi_{xz}$ respectively. More specifically, if it is helpful to see written down, we will have that \begin{align*} \pi_{xy}(x,y,z) &= (x,y) \\ \pi_{yz} (x,y,z) &= (y,z) \\. \pi_{xz}(x,y,z) &= (x,z).\end{align*}
Before we go into the proof of such a bound, let’s use dimensional analysis to figure out what this bound should look like. Namely speaking, we may expect to have a bound of the following form: \[|A| \leq (|\pi_{xy}(A)| \cdot |\pi_{yz}(A)|\cdot |\pi_{xz}(A)|)^{\alpha}\] for some constant $\alpha$.
Why might we expect this? Well, given our set $A$ is arbitrary, we should expect that no particular plane should be favored– i.e. there should be a symmetry to our bounds (as we have in the above formula). Secondly, and perhaps less rigorously– this bound looks the same as in the 2-dimensional case. So, for now, supposing that such a bound holds, let’s figure out what $\alpha$ should be by dimensional analysis. We measure $A$ in cubic inches and the projections (onto the 2-dimensional planes) in square inches. As such, we get that \[(\text{inches}^3) \leq [(\text{inches}^2)\cdot (\text{inches}^2)\cdot (\text{inches}^2)]^\alpha.\]
Hence, to get (at least through dimensional analysis) best bound we can hope for, we may expect $\alpha = 1/2$. In fact, this is the case:
Theorem: Let $A\subset \mathbb{R}^3$ be a finite set of points. Then, \[|A| \leq \sqrt{|\pi_{xy}(A)|\cdot |\pi_{yz}(A)| \cdot |\pi_{xz}(A)|}.\]
We will spend the rest of Part 1 proving this fact, but to do so we will need some new and better ideas. Notice that, it is in fact true that \[A\subset [\pi_{xy}^{-1}(\pi_{xy}(A)) \cap \pi_{yz}^{-1}(\pi_{yz}(A)) \cap \pi_{xz}^{-1}(\pi_{xz}(A))],\] and thusly we automatically have that \[|A| \leq |\pi_{xy}(A)| \cdot |\pi_{yz}(A)| \cdot |\pi_{xz}(A)|,\] but this bound is worse than the one we are trying to obtain (and thusly we will need better ideas).
The “better” idea we will need will be to write $|A|$ as a sum. In particular, consider the function: $\mathbf{1}_A$, which is 1 on the set $A$ and is 0 otherwise. I.e., \[\mathbf{1}_A(x,y,z) = \begin{cases}1 & (x,y,z) \in A \\ 0 & (x,y,z) \notin A\end{cases}.\] This is known as an indicator function, and it is really helpful for our problem because we have that \[|A| = \sum_{x,y,z} \mathbf{1}_A(x,y,z).\] I.e., we have written $|A|$ as a sum that we can now manipulate.
Not only that, but we can similarly define indicator functions for all of the projections of $A$, namely $\mathbf{1}_{\pi_{xy}(A)}$, $\mathbf{1}_{\pi_{yz}(A)}$, and $\mathbf{1}_{\pi_{xz}(A)}$. What can we do with this? Well, we can notice that for all $(x,y,z) \in \mathbb{R}^3$, we have \[\mathbf{1}_A(x,y,z) \leq \mathbf{1}_{\pi_{xy}(A)}(x,y)\cdot \mathbf{1}_{\pi_{yz}(A)}(y,z) \cdot \mathbf{1}_{\pi_{xz}(A)}(x,z).\]
Why is this true? Well, if $(x,y,z)$ is a point in $A$, then by definition $(x,y) \in \pi_{xy}(A)$, $(y,z) \in \pi_{yz}(A)$, and $(x,z) \in \pi_{xz}(A)$, so the left hand side (LHS) of the above inequality is 1 and so is the right hand side (RHS). Note: there may be points where the RHS is 1 but the LHS is 0– Why?? Similarly, if the RHS is zero, then one of the three terms in the product must be zero (say, $\mathbf{1}_{\pi_{xy}(A)}(x,y)$). If this is the case, then it must be the case that $(x,y,z)$ is not a point of $A$ for any $z$! Therefore, when the RHS is zero, the LHS must be zero. This concludes the proof of the above inequality. Using it, we notice that we can use this in what we have proven thus far, namely: \[|A| = \sum_{x,y,z} \mathbf{1}_A(x,y,z) \leq \sum_{x,y,z} \mathbf{1}_{\pi_{xy}(A)}(x,y)\cdot \mathbf{1}_{\pi_{yz}(A)}(y,z) \cdot \mathbf{1}_{\pi_{xz}(A)}(x,z).\]
At this point, I want to use something known as the Cauchy-Schwarz inequality. There are a bajillion (or rather, at least 12) proofs of this inequality (none of which are particularly long, but that I don’t want to write down into this blogpost). Basically, the Cauchy-Schwarz inequality states that you can go from sums of products to products of sums (with certain exponents). In particular, we have that \begin{align*} &\sum_{x,y}\sum_z \mathbf{1}_{\pi_{xy}(A)}(x,y)\cdot \mathbf{1}_{\pi_{yz}(A)}(y,z) \cdot \mathbf{1}_{\pi_{xz}(A)}(x,z) \\ &\leq \left(\sum_{x,y} \mathbf{1}^2_{\pi_{xy}(A)}(x,y)\right)^{1/2}\left(\sum_{x,y} \left(\sum_z \mathbf{1}_{\pi_{yz}(A)}(y,z) \cdot \mathbf{1}_{\pi_{xz}(A)}(x,z)\right)^2\right)^{1/2} := I \times II.\end{align*}
Why was this helpful? Because one can see immediately that $I = \sqrt{|\pi_{xy}(A)|}$! Note: Here, we used that $0^2 = 0$ and $1^2 =1$. So now we just need to bound the term $II$, or rather $II^2$ so we don’t have to carry the squareroot around everywhere. To do so, we can expand the sum in $z$ into a double sum in $z$ and another (dummy) variable $z’$.
In particular, we have that \begin{align*} II^2 &=\sum_{x,y} \left(\sum_z \mathbf{1}_{\pi_{yz}(A)}(y,z) \cdot \mathbf{1}_{\pi_{xz}(A)}(x,z)\right)^2 \\ &= \sum_{x,y}\sum_z \sum_{z’} \mathbf{1}_{\pi_{yz}(A)}(y,z) \cdot \mathbf{1}_{\pi_{xz}(A)}(x,z) \cdot \mathbf{1}_{\pi_{yz}(A)}(y,z’) \cdot \mathbf{1}_{\pi_{xz}(A)}(x,z’). \end{align*} Try to see why the above bound is true! Using this, we have that \begin{align*} &\leq \sum_{x,z}\sum_{y,z’} \mathbf{1}_{\pi_{xz}(A)}(x,z)\cdot \mathbf{1}_{\pi_{yz}(A)}(y,z’). \end{align*} Again, try to see why! Rearranging these sums (now that they are independent of one another), we see that \begin{align*} &= \sum_{x,z} \mathbf{1}_{\pi_{xz}(A)}(x,z)\cdot \sum_{y,z’}\mathbf{1}_{\pi_{yz}(A)}(y,z’) \\ &= |\pi_{xz}(A)| \cdot |\pi_{yz}(A)|.\end{align*} Throwing back in the squareroot, we obtain the desired theorem.
Exercise: Prove that this bound is good by considering a similar example to the 2-dimensional case. Prove that this bound *can* be bad, i.e. that there is a set in which the inequality (while true) is WAAYYY overkill (for a more technical statement, see the analogous 2-dimensional exercise).
Exercise: Depending on your background in calculus, try proving a continuous version of this for “nice enough” sets in $\mathbb{R}^3$. I.e., can you use integration (as opposed to discrete sums) to get rid of the assumption the $A$ is finite?
Exercise: Try generalizing this in higher dimensions! This is known as the Loomis-Whitney inequality. The next difficult case to try perhaps is bounding the volume of a 4-dimensional finite set by the area of it’s projections onto (the 6!) 2-dimensional planes (i.e. the xy, xz, xw, yz, yw, zw-planes). If you find this interesting, consider looking into Alex Iosevich’s “A View From the Top” which is how I learned about this problem.
Part 2: The Lessons (aka the life part)
Part 2a: okay fine I’m not done talking about math yet– but give me a sec.
For those who skipped Part 1, the tldr of the math problem I was talking about was the following: Given some blob out in space, if you know how large it’s shadow is, can you know (roughly) how large the blob is? That’s is; that’s the problem (and it leads to what is known as the Loomis-Whitney inequality).
I first learned this proof (of the 3-dimensional) Loomis-Whitney inequality in the summer after my freshman year when I did a reading program with my (soon to be) research advisor Larry Guth and his graduate student Yuqiu Fu. Immediately, I fell in love with the problem (even if it was already solved by Loomis and Whitney all those years ago).
The reason I love this problem is two-fold. One: I love that this problem uses tools that I think are fundamentally interesting in how useful/simple they are (e.g., an inequality known as the Cauchy-Schwarz inequality, or using indicator functions). Two, and perhaps more fundamentally: I love that I can describe this problem in a single sentence: I want to understand some blob by knowing the shadows of the blob. Bam– that’s it.
And yet, when I look at the proof in all of it’s glory, I think to myself: this proof is ugly as hell. I mean sure! It works! It’s a complete proof! I can write it down completely from beginning to end. I can explain all the tiny steps that go into the overall proof. And I can admire it’s perfect and elegant use of simple inequalities. And yet. And yet.
I look at the proof and think: that was actually really hard to prove algebraically, especially given it was something I expected to be immediately clear.
—
People sometimes ask me how I got into the type of math that I do. And my response is always this story: In some classes, sometimes there is just something that irks me about a proof. I can write it down from start to finish. Examine all it’s details from beginning to end. And still, it feels too complicated. It seems to hard to be “the right way” to prove something. But alas it is. This is a feeling I have felt in many classes, especially at MIT.
Where sometimes, I would solve a homework problem in 18.701: Algebra I, look at it, and think “this must not be the simple way to prove this problem”. And most of the time I would be right. I’d turn to a friend who understood the subject better, and they’d give me a two-line, elegant solution. And then I’d stare at the solution and think to myself: well this seems to be hiding something behind the scenes. Like, there’s some magic that is happening that I don’t see in their two-line proof, and this (in turn) irks me more. Because in both cases, I don’t feel satisfied.
So imagine my surprise when I learn this proof in my reading course with Larry and Yuqiu, and I think to myself the same thing. But this time…. This time when I tell Larry that I think the proof feels too complicated for what we are proving– he says he agrees. That he too has thought about whether or not there is a simpler proof for this statement (and as far as I know hasn’t found one).
This was one of those few moments that really got me hooked into my area of mathematics: the fact that I could ask a question that I only barely knew how to put into words, and have it be something that others have been curious about before too.
Part 2b: okay fine some actual life stuff
I got into math for education. I mean, sure, I liked the subject myself, but part of what I liked most about mathematics was figuring out how to best explain/motivate a concept for other people (and thusly for myself too). This is why I ultimately decided that I wanted to become a professor.
And as a result, my freshman year I really felt this pressure in every class I took:
I’m struggling now so that one day I can explain these concepts to my students.
Just work through it– you need to work through it to be a professor.
Math is hard, but you just gotta get through this.
Get through this.
Get through this.
At first, education felt like my anchor point. Something to aim for and aspire to. But somewhere along the way, the anchor point became a bit difficult for me to hang onto in quite the same way. What was once “Work through this to become a good professor” became
Work through this to get into graduate school.
You have to prove yourself to others.
You have to prove yourself to you.
Struggle through this.
Struggle through this.
Now that I’ve gotten into graduate school– Now that I know where I will be for the next ~6 years of my life– Now that I am nearly ready to graduate from MIT–
—
As a mathematician, I look at the proof of the Loomis-Whitney inequality and think to myself: this is beautiful. As an educator, I’m conflicted. I mean sure– I can motivate why I like the proof as a mathematician, but I couldn’t explain the proof to someone on a walk. And because (for me) mathematics has always been deeply intertwined with education, that bothers me.
But what bothers me more than that, is that for the past couple of years at MIT I’ve felt like I’ve ignored why that bothers me. I’ve ignored the part of me that wants to think about how I present mathematics in a more accessible way (e.g., this blog). I don’t know. Perhaps that isn’t fully coherent.
All of which is to say, I am excited to stop ignoring that irksome feeling in graduate school. Because I made it. In Fall 2025, I will be returning to MIT to pursue my PhD in mathematics.

